阅读:0
听报道
导读:
2015年9月14日,人类首次捕获来自双黑洞合并的引力波,似一声鸣啼,就此开启了引力波天文学的新时代。随着引力波探测水平的不断进步,我们有望在不远的将来听见数以千计的啁啾(zhōu jiū)。
物理学家如今正在思考,如何从这些啁啾所携带的丰富信息中提取双黑洞轨道的形状,进而了解其周边环境的特征。利用这些线索,我们也许有机会解密隐藏在黑暗宇宙中最引人入胜的玄机。
本期《天问专栏》将从一声啁啾中,窥得一丝宇宙的奥秘。
撰文 | 鲜于中之
责编 | 吕浩然

在虚茫无垠的宇宙深处,曾有两颗30倍太阳质量左右的黑洞,彼此环绕,逐渐靠近,经过了不知多久的相伴,终于在几秒钟内完成了最后一千米的冲刺,剧烈地拥抱在一起。随后,相当于3个太阳的质量化为时空的颤栗,飞散开来。这瞬间的能量,比宇宙中所有已知星系发出的光还要强10倍。
此后,时空的涟漪以光速飞行了上亿年,终于在2015年9月14日到达地球。那一天,在美国激光干涉引力波天文台(LIGO)两架巨大且精致的干涉仪中,悬挂的镜面在这涟漪的扰动下出现了异乎寻常的抖动。而抖动的幅度,比原子核的尺寸还要小许多。不过,LIGO的镜面仿佛极端灵敏的鼓膜,足以听清那抖动中所携带的信号,犹如一声短促的啼鸣。这就是人类首次直接观测到的引力波信号,科学家称之为GW150914。
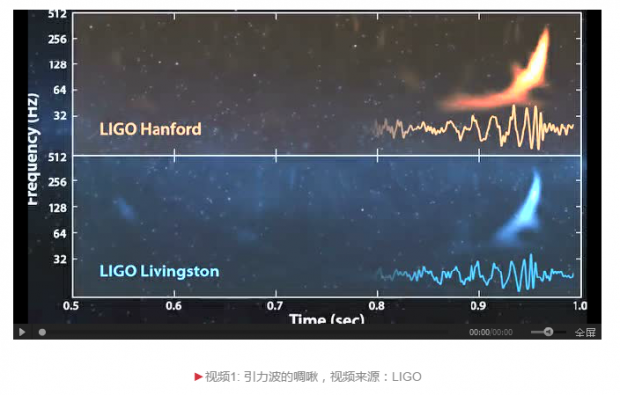
像GW150914这样来自双体系统合并的引力波信号,LIGO和VIRGO目前已公布了六例,其中一例来自一对中子星(GW170817),伴有各波段的光学信号。随着今后LIGO和VIRGO灵敏度的进一步升级、以及更多地面与空间引力波探测器的加入,我们对引力波的听觉将会愈加灵敏。
据现有观测结果预计,在LIGO以接近其设计灵敏度的水平运行时,一年的观测时间将能捕获成百上千的双黑洞合并。这样的统计量将在真正意义上开启引力波天文学和宇宙学的新时代。自此以往,人类就拥有了一种倾听宇宙的全新感官,帮助我们探索视线难以触及的未知世界。
你也许会好奇,同样是双黑洞合并,一次事件与一千次事件,有何区别?收集一千个事例,难道只是为了将爱因斯坦百年前的预言验证一千次?若是这样,这篇文章就要到此为止了。实际上,相较于个别的独立事件,物理学家对事件背后的统计关联更感兴趣,因为这些关联也许能帮助我们回答一些非常基本的问题。在物理学家看来, 阵阵啼鸣的背后另有玄机。也许,它们能帮助我们检验各种关于万有引力的基本理论,或者,它们能帮助我们识别暗物质和暗能量的踪迹。
对于这些基本的问题,我们目前还无从回答。但无论如何,它们的答案必须从倾听和分析引力波的声音中揭晓,而这就需要我们对双黑洞合并的啼鸣有足够好的理解。因此,我们将在这篇文章中从一个更具体地问题出发,为读者展示如何通过听辨双黑洞合并的啼鸣来获知它们背后的物理。这个问题很好陈述:就好像我们从一个人说话的口音大致可以推测他的故乡一样,我们想知道,双黑洞合并的鸣啼声的音调和音色中隐藏着多少关于它们“故乡”的讯息。为了解释这个问题,让我们先对黑洞的啁啾做一点初浅的解析。
啁啾物理学
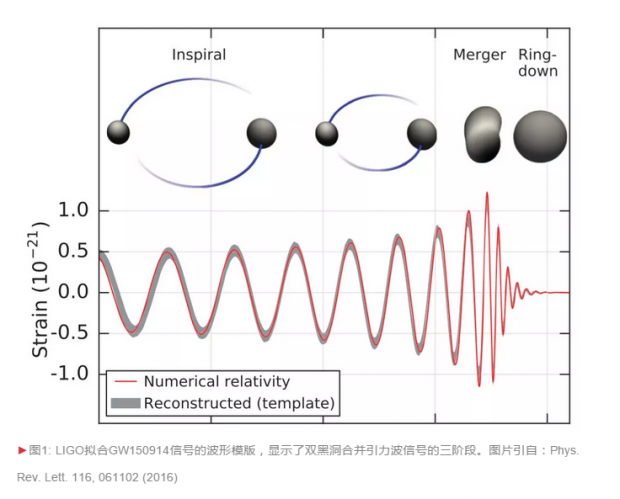
从双黑洞合并的引力波波形中(图1),我们可以辨认出三个阶段。在持续时间最长的第一阶段,引力波的幅度缓慢增加、频率逐渐升高。这一阶段称为“旋近”(图1中inspiral部分),因为它对应于一对黑洞在各自引力的作用下围绕对方相互旋转。
与此同时,它们的间距由于引力波辐射带走能量而逐渐缩小。LIGO只能捕捉到这一极为漫长的阶段最后的尾声。这是因为,如同人耳有一定的听觉范围(约20Hz至20000Hz),LIGO的听觉范围也有限(约10Hz至数千Hz)。
在短暂的第二阶段,引力波的波幅达到极大,呈现出剧烈的振荡,这对应于双黑洞快速的“合并”(图1中merger部分)。在第三阶段,波幅迅速衰减,最终归于静寂。这对应于双黑洞合并的产物通过引力波释放能量,最终形成一个稳定的新黑洞。因此,这最终的阶段称为“铃宕”(图1中ringdown部分)。
在物理学家看来,“合并”阶段的信号最为复杂难解。由于此时黑洞的相互旋转速度快、引力强,通常的低速弱场近似都失效,因而只能在广义相对论的框架下,通过数值计算的方式进行研究。与此相对,我们有足够好的近似理论处理旋近和铃宕两个阶段,因而有机会从中提取很多宝贵的信息。比如,铃宕的过程,就可以看作高度激发的黑洞向基态衰变的过程,因此铃宕的信号可以帮助我们了解黑洞激发态的结构,进而了解黑洞自身的结构。
而在旋近阶段,双黑洞间的引力不算强,旋转的速度也不太快。比如,一对总质量为太阳20倍的双黑洞在进入LIGO的观测窗口时,其旋转速度大致为光速的六分之一。因此,我们可以用牛顿力学作为零级近似,将相对论效应视作微扰,按黑洞速度与光速的比值作系统的微扰展开。这种方法,叫做“后牛顿展开”(post-Newtonian expansion)。
用牛顿力学处理双体系统的运动,就是后牛顿展开的领头阶。在这一级近似下,处于圆轨道的双体系统,激发的引力波频率恰好是绕轨道旋转频率的两倍。由于引力波会从双体系统中带走能量,随着时间的推移,二者的间距会逐渐缩小,旋转速度逐渐加快,频率逐渐升高。
因此,引力波在领头阶呈现出频率随时间升高的单频音,这就是双黑洞“啁啾信号”(chirp signal)的由来。从啁啾音调上扬的快慢,我们可以“听”出双黑洞总体的轻重,而从这信号幅度的大小,则可以听出双黑洞的远近——因为振幅在传播的过程中会衰减,与传播的距离成反比。
领头阶的引力波只能告诉我们两颗黑洞总体有多重。要为每颗黑洞单独称重,需要进入后牛顿展开的下一阶。后牛顿展开的高阶修正里隐藏着丰富的信息,除了每颗黑洞的质量外,还有它们的自旋。对于双中子星系统,高阶修正里还携带着关于中子星物态的信息。不过,我们不再继续讨论高阶修正,而是在领头阶,讨论一个更有趣的问题:如何改变双体系统引力波的音色。
循声辨其形
人们能够轻易地分辨出小提琴和长笛的声音,是因为它们有不同的音色。音色反映了声波中不同频率成分的相对比重,对于引力波亦是如此。上文提到,啁啾信号在领头阶是单频信号,仿佛一支音调随时间升高的音叉。
这单频信号背后的原因在于,双黑洞沿圆轨道的旋转在一个周期内近乎匀速。倘若将轨道改为椭圆,黑洞的速度在同一周期内就会有快有慢。这种不均匀的运行,就会产生频率为轨道频率各个正整数倍的谐波,黑洞就有了不同的音色。
不难想象,黑洞轨道越扁,引力波的频谱就越偏离圆轨道的单频信号。因此,我们从啁啾信号的音色,就可以辨认出轨道的形状。椭圆轨道“扁”的程度由离心率刻画。离心率的取值在0到1之间,0对应于正圆,而越接近1就越扁。下面的视频是用后牛顿近似的领头阶计算模拟出的不同离心率轨道的啁啾,你听出它们的区别了吗?(视频2)

实际上,在LIGO已公布的双体合并事件中,引力波信号都十分接近完美的圆轨道,没有明显的离心率。比如,GW150914中双黑洞轨道的离心率小于0.1。然而,这并不出乎意料。根据牛顿力学,能量决定了椭圆轨道的半长轴,角动量则决定了它的离心率。引力波不仅会从双体系统中带走能量,也会带走角动量,因此在缩小轨道尺寸的同时,也会改变轨道的形状,仿佛在不停地“打磨”它。
计算显示,在漫长的旋近过程中,引力波会非常高效地将椭圆轨道磨得越来越圆。由于LIGO只能探测该过程的最后一瞬,即使双体系统在更早的某一时刻具有相当大的离心率(即轨道呈非常扁的椭圆),经过引力波漫长地打磨,在进入LIGO的观测范围之后,原有的离心率也早已被打磨干净,难觅踪影。
所以,如果LIGO听见了椭圆轨道的啁啾,大体上只有两种可能。或者,这对黑洞的轨道曾经具有非常大的离心率,直到进入LIGO窗口时还没有被引力波打磨殆尽;再或者,两颗黑洞原本不是一对,它们只是碰巧,几乎头对头地撞在一起,同时闯入LIGO的听觉窗口。
对于孤立的双黑洞而言,这两种可能性都极难实现。粗略地讲,它们都要求双黑洞在形成的时刻对彼此有近乎完美的瞄准:想象在太阳和地球的位置上各有一颗黑洞飞向彼此。如果它们在进入LIGO窗口时具有可观的离心率,就必须将瞄准的误差控制在千公里的量级。换言之,百步穿杨还不够,你得在百步之外打中树叶上一条指定的叶脉才行。
看来,如果我们在LIGO中观测到椭圆轨道的双体系统,很可能意味着这对双体系统并不孤立,而是受到了周遭环境的影响。不过,通过周边的物质分布来扰动双黑洞的轨道,也是极为困难的事情。因为,双黑洞系统异常地致密而“坚硬”。
这并不难理解:当一对总质量数十倍于太阳的黑洞进入LIGO的探测器时,它们的轨道间距只有区区几千公里。要知道,太阳的半径也有70万公里。所以,就算你在双黑洞周围堆满太阳,其密度也只有双黑洞系统的亿分之一。
或许你已经想到,我们可以在双黑洞信号进入LIGO探测器之前,在它们轨道间距更大、还不那么坚硬的时期去干扰它们、为它们的轨道“注入”额外的离心率。这当然可能,可是别忘了,引力波在一刻不停地打磨轨道。你扰动得越早,就得克服越长久的打磨。
因此,通过扰动注入的离心率就必须足够大才行。可是,期望随机偶遇的第三者来注入足够大的离心率,无异于守株待兔。事实上,更好的办法是,通过一种持续的扰动,以相干共振的方式来注入离心率。这就是下一小节要介绍的“古在机制”(Kozai mechanism)。
黑洞三重奏
古在机制,是通过第三者的潮汐力为双体系统注入离心率的一种方式,最初由物理学家米哈伊尔·里多夫(Mikhail Lidov)和古在由秀(Yoshihide Kozai)发现于上世纪六十年代[1]。为了解释这种机制,让我们将眼下的双体系统看作整体,称为“小双体”,并将它与居于远处的第三者一道,看作一个更大的双体系统,称为“大双体”。
这样的三体系统,称为“分级三体”(hierarchical triple)。它其实很常见:太阳、地球、月亮就可以看作分级三体。其中,地球与月亮构成小双体,而地月系统作为整体,与太阳一道构成大双体。
小双体系统两个成员的空间位置不同,感受到第三者的引力也不同。两者感受的引力差,就是第三者对小双体系统的潮汐力。古在机制说,当小双体的轨道面相对于大双体的轨道面有很大的倾角时(大于39度),第三者的潮汐力就会触发小双体轨道的离心率与倾角的周期振荡。
特别是,如果初始的轨道倾角非常大,比如说90度左右,那么小双体轨道的离心率就可以非常接近1,也就是变得非常扁(图2)。幸好,月球轨道相对于黄道面的倾角只有5度,不足以激活古在机制。否则,月球轨道很大的离心率意味着地月距离将发生大幅振荡,对地球上的生物无疑是一场灾难。
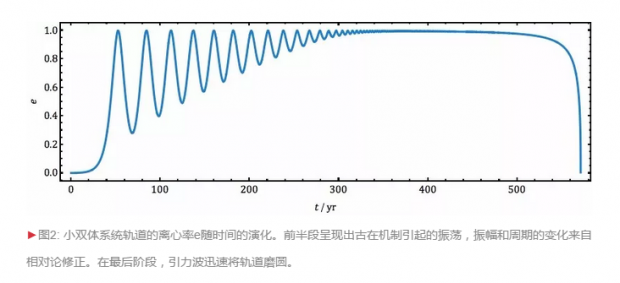
古在机制是合成高离心率双体系统的理想方式,然而要实现它就需要分级三体。在星系中,我们该去哪里寻找这样的三体系统呢?构成分级三体的恒星系统在星系盘中并不罕见,可是,要找到LIGO足以观察到的三黑洞系统,就不那么容易了。要想大量合成这样的黑洞三体,就必须借助非常稠密的环境。在星系里,物质分布最密集的区域要属球状星团和星系中心(图3)。

球状星团,是散布在星系晕中的球状密集区域,它们可能是星系中最早形成、最古老的群体,其中密布着大量恒星质量或更重的天体。据理论推测,球状星团可能富含双体黑洞,而两个黑洞双体系统通过散射,就有机会合成一个稳定的分级三体系统。因此,球状星团被认为是合成三体黑洞的理想场所[2]。
另一方面,星系的中心一般会有一个特大质量黑洞(supermassive black hole),质量可达太阳的十万倍到十亿倍。在特大质量黑洞附近,也许会有丰富的恒星质量级别的双黑洞系统。这些双黑洞与中心的大黑洞一道,也构成分级三体系统[3]。
在球状星团和星系中心这些稠密且富含双黑洞的区域,双黑洞都有可能通过古在机制获得很高的离心率。双体系统的高离心率将会大幅增强引力波的辐射,继而提高双黑洞间距缩小的效率、缩短黑洞合并所需的时间。据推测,在LIGO与未来的引力波探测器将能捕捉到的双体合并事件中,由古在机制造成的椭圆轨道信号会有相当可观的贡献。
天籁交响曲
由上可见,LIGO中音色异乎寻常的椭圆轨道双体系统,很可能来自星系中最为稠密的区域。当我们拥有足够的统计量时,就能够寻找这些事件中离心率的统计分布以及它们与其它参数的关联。由于这些关联非常依赖双黑洞周遭的环境,对它们的测量和分析就可以帮助我们分辨这些双黑洞的合成途径,甚至帮助我们提取双黑洞所在环境的信息。
我们现在对特大质量黑洞附近的物质分布还知之甚少:恒星如何分布?黑洞如何分布?更进一步:不同的暗物质模型对这些分布会有怎样的贡献、对引力波信号各参数的统计关联会有怎样的影响?所有这些,在目前都还是有待探索的开放问题。
物理学家通常使用大量的数值模拟来推测这些条件对可观测量的影响。与此同时,也有研究开始试图用解析的方法将双黑洞合成时的初条件直接映射到可观测量的分布,以期获得双黑洞演化更清晰的物理图像,并提高分析的效率[4]。
这些研究显示,通过古在机制等方式造就的椭圆轨道双体系统在进入LIGO探测器之后,大多数事例的离心率仍然很小。非常粗略地估计,90%以上事例在进入LIGO窗口时的离心率会小于0.1,而LIGO能够分辨的最小离心率也许可达百分之几。因此,LIGO有望绘制出一幅漂亮的离心率分布图,只是它并不完整。
受探测频率范围所限,LIGO这类地面探测器只能听见双黑洞合并刹那的绝唱。而在此之前,这些双体系统在其漫长的生命历程中也在不断释放频率更低、持续时间更长的引力波,如同暗弱而低沉的笛声。要捕捉这些信号,就必须借助空间引力波探测装置。
在地面和空间的引力波探测器的协同观测下,我们将能够通过多个声道,监听双黑洞系统更长、更完整的生命历程。我们还将有机会捕捉到其它种类的引力波源,更全面地还原来自宇宙暗处的引力波交响曲。而LIGO捕捉到的啁啾,只不过是这部交响曲的高声部。
言及此处,让我们不要忘记,宇宙中大约95%的能量都隐没在暗物质和暗能量的黑暗世界中,我们对它们零星的了解,全都依赖它们与可见物质的引力作用。引力波天文学与宇宙学的重要意义,由此不言而喻。说不定,这部用引力波演奏的天籁交响曲,能够帮助我们理解黑暗宇宙最深刻的奥秘也未可知。
作者简介
· 鲜于中之,物理学博士。2015年毕业于清华大学,目前在哈佛大学从事博士后研究,研究方向为粒子物理和宇宙学理论,最近的研究兴趣包括暴胀理论、原初扰动与新物理、引力波等。
参考文献:
[1] M. L. Lidov and S. L. Ziglin, Celestial Mechanics, 13, 471 (1976)
[2] L. Wen, Astrophys. J. 598, 419 (2003) [arXiv:astro-ph/0211492].
[3] F. Antonini and H. B. Perets, Astrophys. J. 757, 27 (2012) [arXiv:1203.2938 [astro-]].
[4] L. Randall and Z. Z. Xianyu, Astrophys. J. 853, 93 (2018) [arXiv:1708.08569 [gr-qc]]; arXiv:1802.XXXXX.

话题:
0
推荐
财新博客版权声明:财新博客所发布文章及图片之版权属博主本人及/或相关权利人所有,未经博主及/或相关权利人单独授权,任何网站、平面媒体不得予以转载。财新网对相关媒体的网站信息内容转载授权并不包括财新博客的文章及图片。博客文章均为作者个人观点,不代表财新网的立场和观点。




 京公网安备 11010502034662号
京公网安备 11010502034662号 