编者按：

 

浙江大学数学学院教授、诗人蔡天新最新出版力作——《数学简史》。《知识分子》征得作者本人及出版社同意，分三篇文章连载该书的第八章：《抽象化：20世纪以来》。

 

今天继续推送《数学简史》第八章第二节：《数学的应用》。

 

撰文 | 蔡天新（浙江大学数学学院教授）

责编 | 吕浩然

 

●　●　●

 

理论物理学

 

现在，我们来谈谈数学向人类文明的其它结晶（科学）的渗透。先来看物理学，18世纪是数学与经典力学相结合的黄金时代，19世纪数学主要应用于电磁学，产生了剑桥大学数学物理学派，其中最具代表性的成就是麦克斯韦（Maxwell，1831—1879）建立的电磁学方程组，由4个简洁的偏微分方程组成。据说麦克斯韦最初得到的方程组比较复杂，因为他相信表达物理世界的数学应该是美的，因而推倒重来。

 

麦克斯韦是苏格兰人，这个流行男子穿格子短裙的民族所产生的伟大发明家按人口比例堪称世界之最。在麦克斯韦之前有（实用）蒸汽机发明人瓦特（Watt，1736—1819），之后有电话发明人亚历山大·贝尔（Bell，1847—1922）、胰岛素发明人麦克劳德（Macleod，1876—1935，与人合作）、青霉素发明人弗莱明（Fleming，1881—1955）、电视发明人贝尔德（Baird，1888—1946）。

 

此外，还有第一个将经济理论完整化和系统化的亚当·斯密（Adam Smith，1723—1790）。斯密的代表作《国富论》的中心思想是：看似混乱的自由市场实际上有一种自动调控机制，它倾向于以最合适的数量生产那些社会上最受欢迎和最需要的产品。

 

►爱因斯坦的数学老师闵可夫斯基

 

进入20世纪以后，数学相继在相对论、量子力学以及基本粒子等理论物理学领域得到应用。1908年，德国数学家闵可夫斯基提出了空间和时间的四维时空结构R(3,1)，即通过（c为真空中的光速）

 

 

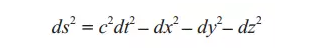
为爱因斯坦（Einstein，1879—1955）的狭义相对论（1905）提供了最适用的数学模型，这种结构后来被称为“闵可夫斯基空间”。有趣的是，闵可夫斯基对他早年的学生爱因斯坦的数学才能却毫无印象。

 

有了这个模型以后，爱因斯坦又进一步研究了引力场理论。等到1912年夏天，他已经概括出这一理论的基本原理，可是由于他只会使用一些最简单的数学工具，甚至微积分的方法也不会用（他自称那样会使读者被惊呆），自然难以提炼出方程来。这个时候爱因斯坦在苏黎世遇到一位数学家，后者帮助他学会了以黎曼几何为基础的微分学，后来他把它叫作“张量分析”。经过三年多的努力，在1915年11月25日发表的一篇论文中，爱因斯坦给出了引力场方程：

 

 

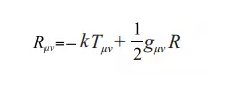
其中gμv是度量张量，k为常数。爱因斯坦指出，“有了这个方程，广义相对论作为一种逻辑结构终于成立了！”

 

值得一提的是，虽然爱因斯坦在1915年创立了广义相对论，但他的工作成果发表于1916年。巧合的是，几乎是同时，另一个德国人、数学家希尔伯特沿着另一条道路也得到了上述引力场方程。希尔伯特采用的是公理化方法，同时运用了诺特关于连续群的不变量理论。他向哥廷根科学院提交这篇论文的时间是1915年11月20日，发表论文的时间也比爱因斯坦早了5天。

 

依照爱因斯坦的广义相对论，时空整体上是不均匀的，只在微小的区域内例外。在数学上，这个非均匀的时空可以借助下列的黎曼度量来描述：

 

 

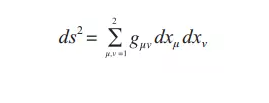
广义相对论的这个数学描述第一次揭示了非欧几何学的现实意义，也成为历史上最伟大的数学应用例子之一。可是，与建立万有引力定律的牛顿相比，爱因斯坦稍显逊色，因为牛顿力学的数学基础——微积分是由牛顿自己创立的。

 

与相对论不同，量子力学与一群物理学家的名字相联系。普朗克（Planck，1855—1947）、爱因斯坦、玻尔（Bohr，1855—1962）是开拓者，薛定谔（Schrödinger，1887—1961）、海森堡（Heisenberg，1901—1976）、狄拉克等分别以波动力学、矩阵力学和变换理论的形式建立起量子力学。为了将这些理论融合成统一的体系，需要新的数学理论。希尔伯特使用积分方程等分析工具，冯·诺依曼进一步借助希尔伯特空间理论，去解决量子力学的特征值问题，并最终将希尔伯特的谱理论推广到量子力学中经常出现的无界算子情形，从而奠定了这门学科的严格的数学基础。

 

在20世纪下半叶，还有多项物理学的工作需要应用抽象的纯粹数学，例如著名的规范场理论和超弦理论。1954年，杨—米尔斯理论的提出揭示了规范不变性可能是自然界中所有4种力（电磁力、引力、强力和弱力）相互作用的共性，这使得已经存在的规范场理论重新引起人们的注意，并试图用这个理论来统一自然力的相互作用。

 

结果，数学家们很快发现，统一场论所需要的数学工具——纤维丛微分几何早就有了，杨—米尔斯方程实际上是一组偏微分方程，对它们的进一步研究也推动了数学的发展。1963年被证明的阿蒂亚—辛格指标定理也在杨—米尔斯理论中获得重要应用，成为连接纯粹数学和理论物理的又一座桥梁，其研究方法涉及分析学、拓扑学、代数几何、偏微分方程和多复变函数等诸多核心数学分支，因而常被用来论证现代数学的统一性。

 

超弦理论或弦理论兴起于20世纪80年代，它把基本粒子看作一些伸展的一维弦线般的无质量的实体（其长度约为10–33厘米，被称为普朗克长度），以代替其他理论中所用的在时空中无尺寸的点。这个理论以引力理论、量子力学和粒子相互作用的统一数学描述为目标，成为数学家与物理学家携手合作的一个最活跃的领域，其中所用到的数学涉及微分拓扑、代数几何、微分几何、群论、无穷维代数、复分析和黎曼曲面上的模理论等。可以想象，与它相联系的物理学家和数学家不计其数。

 

生物学和经济学

 

除了物理学以外，数学还在其他自然科学和社会科学领域发挥了重要作用。限于篇幅，我们仅以生物数学和数理经济学为例。与物理学相比，生物学是一门年轻的学科，在17世纪显微镜发明以后才真正步入正轨，但它和物理学是自然科学的两个最重要的分支。生物学研究中数学方法的引进也相对迟缓，大约始于20世纪初。多才多艺的英国数学家皮尔逊（Pearson，1857—1936）率先将统计学应用于遗传和进化问题的研究，并于1899年创办了《生物统计》杂志，这是最早的生物数学杂志。

 

1926 年，意大利数学家沃尔泰拉（Volterra，1860—1940）提出了下列微分方程，成功地解释了地中海中不同鱼种周期消长的现象，其中x表示被食小鱼数，y表示食肉大鱼数。这个方程组也被称为“沃尔泰拉方程”，它开了用微分方程建立生物模型的先河。

 

 

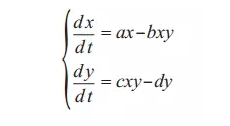
20 世纪50年代，在英国和美国出现了两项轰动性的成果，即描述神经脉冲传导的数学模型霍奇金—赫胥黎方程（此赫胥黎为安德鲁·赫胥黎，他是达尔文进化论支持者托马斯·赫胥黎之孙、小说家阿道司·赫胥黎之弟）和视觉系统侧抑制作用的哈特兰—拉特利夫方程，它们都是复杂的非线性方程，引起了数学家和生物学家的兴趣。有意思的是，前三位分别因此获得1963年和1967年的诺贝尔生理学或医学奖，而拉特利夫（Ratliff，1919—1999）只因为这个方程和作为哈特兰（Hartline，1903—1983）的前同事被人们记住。

 

 

 

1953 年，即霍奇金—赫胥黎方程诞生的第二年，美国生物化学家沃森（Watson，1928—）和英国物理学家克里克（Crick，1916—2004），发现了脱氧核糖核酸（DNA）的双螺旋结构，这不仅标志着分子生物学的诞生，也把抽象的拓扑学引入了生物学。因为在电子显微镜下可以看到，双螺旋链有缠绕和纽结，这样一来，代数拓扑学的纽结理论便有了用武之地，并应验了一个多世纪前高斯的预言。1984年，新西兰出生的美国数学家琼斯（Jones，1952—）建立了关于纽结的不变量——琼斯多项式，帮助生物学家对在DNA结构中观察到的纽结进行分类，琼斯也因此获得了1990年的菲尔兹奖。

 

沃森和克里克获得了1962年的诺贝尔生理学或医学奖，但他们的发现的意义还没有得到充分认识。这里我想多说几句。先用物理学来做参照，它主要探讨宏观世界（原子内部结构的重要性也在于核聚变和核裂变产生的巨大能量），而生物学则侧重研究微观的事物（细胞和基因）。达尔文的进化论和伽利略的自由落体运动定律一样，主要表现了生命和物体运动的外在规律，而牛顿的万有引力定律则发现了物体乃至宇宙运动的内在规律和原因，与此相对应的生物学成就则是揭示了生命奥秘的DNA双螺旋结构。值得一提的是，沃森和克里克是在他们平日和同事们常去的剑桥老鹰酒吧宣布这一里程碑式的发现的。

 

1979 年的诺贝尔生理学或医学奖由两位非本行的专家一起获得，即南非出生的美国物理学家科马克（Cormack，1924—1998）和英国电器工程师豪斯菲尔德（Housfield，1919—2004）。在开普顿一家医院的放射科做兼职时，身为物理学讲师的科马克就对人体软组织和不同密度组织层的X射线成像问题产生了兴趣，到美国任教后，他建立起计算机扫描的数学基础，即人体不同组织对X射线吸收量的计算公式。这个公式建立在积分几何的基础之上，解决了计算机断层扫描的理论问题。这项工作促使豪斯菲尔德发明了第一台计算机X射线断层扫描仪，即CT扫描仪，并在临床试验中取得成功。

 

下面我们要谈的是数理经济学，这门学科是由匈牙利数学家冯·诺依曼开启的。他在与人合著的《博弈论与经济行为》（1944）中提出竞争的数学模型并应用于经济问题，这成为数理经济学的开端。整整半个世纪以后，美国数学家纳什（Nash，1928—2015）和德国经济学家泽尔藤（Selten，1930—）因为博弈论研究获得诺贝尔经济学奖。纳什患有精神疾病，是被改编成电影的小说《美丽心灵》的主人公原型，他建立了纳什均衡理论，解释博弈双方的策略和行动。纳什因为在非线性偏微分方程方面所做的贡献而获得数学界的至高荣誉——阿贝尔奖，则是在他生命的最后一年。

 

►电影《美丽心灵》主人公原型纳什

 

如果说前苏联数学家康托罗维奇（Kantorovich，1912—1986）的线形规划论和荷兰出生的美国经济学家库普曼斯（Koopmans，1910—1985）的生产函数所用的数学理论还比较简单（他们因为在资源最佳配置理论方面的贡献获得1975年的诺贝尔经济学奖），那么法国出生的美国经济学家德布鲁（Debreu，1927—2004）和另一位美国经济学家阿罗（Arrow，1921—2017）所用的凸集和不动点理论就较为深刻了，他们建立的均衡价格理论的后续研究使用了微分拓扑、代数拓扑、动力系统和大范围分析等抽象的数学工具。有意思的是，阿罗和德布鲁获得诺贝尔经济学奖却相隔多年（分别是在1972年和1983年）。

 

20 世纪70年代以来，随着随机分析进入经济学领域，尤其美国经济学家费希尔·布莱克（Black，1938—1995）和加拿大出生的美国经济学家斯科尔斯（Scholes，1941—）将期权的定价问题归结为一个随机微分方程的解，并导出与实际较为吻合的期权定价公式，即布莱克—斯科尔斯公式。在此以前，投资者无法精确地确定期权的价格，而这个公式把风险溢价因素计入期权价格，从而降低了期权投资的风险。后来美国经济学家默顿（Merton，1944—）消除了许多限制，使得该公式亦适用于金融交易的其他领域，如住房抵押。1997年，默顿和斯科尔斯分享了诺贝尔经济学奖。

 

可是，进入21世纪以来，美国发生了次贷金融危机，严重影响了世界经济的发展。在正常情况下，客户一般向银行申请贷款。可是，一部分客户出于信用条件差或其他原因，银行不愿意与他们签订贷款协议。于是，就有贷款机构发放信用要求宽松但利率较高的贷款。次级贷款蕴含较大的违约风险，主要原因在于其衍生产品。有关部门不愿意独自承担风险，往往会将这些产品打包出售给投资银行、保险公司或对冲机构。这些衍生品看不见摸不着，其价格以及打包方式无法通过人为的简单判断来确定，这就催生了一个新兴的数学分支——金融数学。

 

在衍生品的定价过程中，有两个非常重要的参数，即折现率和违约概率，前者基于某个随机微分方程，后者服从泊松分布。通过遭遇这次世界性的金融危机，人们发现这两种数学手段以及其他估价手段还需要更精准。20世纪90年代，同一年（1947）出生的中国数学家彭实戈和法国数学家巴赫杜（Pardoux）合作创立了倒向随机微分方程，现已成为研究金融产品定价的重要工具。

 

18世纪初，雅各布·伯努利说过，从事物理学研究而不懂数学的人，实际上处理的是意义不大的事情。到了21世纪，金融业或银行业也出现了这种情况，有着200多年历史的美国花旗银行宣称，他们有70%的业务依赖于数学，同时强调如果没有数学花旗银行就不可能生存下去。

 

最后，值得一提的是，康托罗维奇的线性规划论是运筹学中最早成熟的研究内容和分支之一。运筹学可以定义为，管理系统的人为了获得关于系统运行的最优解而必须使用的一种科学方法，主要依赖于数学方法和逻辑判断。与运筹学几乎同时脱胎于第二次世界大战的应用数学学科还有控制论和信息论，其创始人分别是美国数学家维纳（Wiener，1894—1964）和香农（Shannon，1916—2001），两人退休前都在麻省理工学院任教，也都是公众人物。维纳18岁就获得哈佛大学博士学位，出版过两本自传——《昔日神童》和《我是一个数学家》；香农则被誉为数字通信时代的奠基人。

 

在维纳看来，控制论是一门研究机器、生物社会中的控制和通信的一般规律的科学，是研究动态系统在变的环境条件下如何保持平衡或稳定状态的科学。他创造了cybernetics这个词，希腊文原意为“操舵术”，就是掌舵的方法和技术的意思。在柏拉图的著作中，常用它来表示管理人的艺术。信息论是一门用数理统计方法来研究信息的度量、传递和变换规律的科学。

 

需要注意的是，这里的信息指的不是传统的消息，而是一种秩序的等级或非随机性的程度，可以测量或用数学方法处理，就像质量、能量或其他物理量一样。

 

计算机和混沌理论

 

一般来说，计算机是指能接收数据，按照程序指令进行运算并提供运算结果的自动电子机器。在计算机的历史上，起重要革新作用的几乎全是数学家。直到20世纪70年代末，中国大学里的电子计算机专业还大多设在数学系，就像康德时代数学隶属于哲学系一样。可是如今，多数大学都有了一两个计算机学院。用机器来代替人工计算，一直是人类的梦想。

 

或许最早使用算盘的并非中国人，但长期以来使用最广泛的当属中国的算盘。在明代（1371）出版的一本书里，就有十档算盘的插图，但它的实际发明时间远在此之前。数学家程大位（1533—1606）的《算法统宗》（1592）详述了珠算的规则、口诀和方法，标志着珠算的成熟。这本书也流传到朝鲜和日本，使得算盘在这两个国家十分流行。

 

第一个提出机械计算机设计思想的是德国人席卡德（Schickard，1592—1635），他在与开普勒通信时阐述了这一想法。第一台能进行加减计算的机械计算机是由帕斯卡发明的（1642），30年后莱布尼茨制造出一台能进行乘除和开方运算的计算机。

 

使计算机拥有能对数据进行各种运算的装置，是向现代计算机过渡的关键一步，由英国数学家巴贝奇（Babbage，1792—1871）首先迈出，在数论里有一个与二项式系数有关的同余式用他的名字命名。巴贝奇设计的“分析机”（1834）分为运算室和存储库，外加一个专门控制运算程序的装置，他曾设想根据穿孔卡片上的“0”和“1”来控制运算的顺序，这无疑是现代电子计算机的雏形。

 

►邮票上的巴贝奇

 

遗憾的是，即便巴贝奇付出后半生的绝大多数精力和财产，甚至失去剑桥大学的卢卡斯教授职位，也没几个人能理解他的思想。据说真正支持他的人只有三个：他的儿子——巴贝奇少将（在父亲去世后还为分析机奋斗了许多年）、未来的意大利总理和诗人拜伦（Byron，1788—1824）的女儿阿达。

 

阿达（Ada，1815—1852）是拜伦和妻子的独生女，她为某些函数编制了计算程序，可谓开现代程序设计之先河。由于时代的局限性，巴贝奇分析机的设计方案在技术实施上遇到了巨大的障碍，他借助通用程序控制数字计算机的天才设想，要再过一个多世纪才能实现。

 

20 世纪以来，科学技术的迅猛发展带来了堆积如山的数据问题，尤其是在“二战”期间，军事上的计算需要更使计算速度的改进成为燃眉之急。起初，人们采用电器元件来代替机械齿轮。1944年，美国哈佛大学的数学家艾肯（Aiken，1900—1973）在IBM（国际商业机器公司）的支持下设计和制造出世界上第一台能实际操作的通用程序计算机（占地170平方米），只部分使用了继电器，不久后他又制成了一台全部用继电器的计算机。与此同时，在宾夕法尼亚大学，人们用电子管来代替继电器，于1946年造出了第一台通用电子数字积分计算机（ENIAC），效率提高了1000倍。

 

1947年，数学家冯·诺依曼（Neumann，1903—1957）提出了把ENIAC使用的外插程序改为存储程序的想法，按照这种想法制成的计算机能按存储器中的指令进行操作，从而大大加快了运算进程。1946年，他与人合作发表论文，提出了并行处理和存储数据计算机的综合设计理念，对后来的数字计算机的设计产生了深远影响。冯·诺依曼出生在布达佩斯，属于多才多艺的那类学者，在数学、物理学、经济学、气象学、爆炸理论和计算机领域都取得了卓越的成就。据说他是在火车站等车时遇见了ENIAC的设计师，后者向他讨教计算机的技术问题，从而激起了他的兴趣。

 

►冯·诺依曼和他的电子计算机

 

►英国萨里大学的图灵铜像

 

另一位对计算机设计理念做出杰出贡献的是英国数学家图灵（Turing，1912—1954），他为了解决数理逻辑中的基本理论问题——相容性，以及数学问题的机器可计算性的判定，而提出了他的“理想计算机”模型。直到今天，数字计算机都没有跳出这个理想模型的范畴：

 

输入/输出装置（带子和读写头）、存储器和控制器。

 

图灵还研究过可以制造出能思考的计算机的理论，这方面的构想已成为人工智能研究的基础。可惜的是，图灵后来因为不堪忍受对其性取向进行的强迫治疗，吃下用氰化物溶液浸泡过的苹果而自杀。为了纪念图灵，1966年，英特尔公司出资设立了“图灵奖”，这是计算机领域的最高奖项。1976年创建的苹果电脑公司以一只被咬了一口的苹果作为标志，这家以推出iPhone手机和iPad平板电脑风靡全球的公司的信念是：只有不完美才能促使进步去追求完美。

 

虽然数字计算机已历经四代的发展，但从电子管、晶体管到集成电路、超大规模集成电路，均是采用二进制拨码开关。这一点不会改变，即使将来有一天，电子计算机被取代（比如量子计算机）。这自然与19世纪英国数学家布尔（Boole，1815—1864）所创立的布尔代数的符号逻辑体系分不开，他完成了两个世纪前莱布尼茨未竞的事业，即创立了一套表意符号，每一个符号代表一个简单的概念，再通过符号的组合来表达复杂的思想。

 

布尔出身贫寒，他的父亲是一个补鞋匠，他主要通过自学成材，后来成为爱尔兰皇后学院（现名为科克大学）的数学教授，并入选英国皇家学会。不幸的是，布尔49岁那年因淋雨患肺炎去世。当年早些时候，他的小女儿出世，她便是小说《牛虻》的作者伏尼契（Voynich，1864—1960）。

 

作为抽象数学应用的一个光辉典范，计算机也已成为数学研究本身的有力工具和问题源泉，并推动了一个新的数学分支——计算数学的诞生。它不仅设计、改进各种数值计算方法，还研究与这些计算有关的误差分析、收敛性和稳定性等问题。冯·诺依曼是这门学科的奠基人之一，不仅与人合作建立了全新的数值计算法——蒙特卡罗方法，还领导一个小组利用ENIAC首次实现了数值天气预报，后者的中心问题是求解有关的流体力学方程。值得一提的是，20世纪60年代，中国数学家冯康（1920—1993）独立创建了一种数值分析方法——有限元法，可用于包括航空、电磁场和桥梁设计等在内的工程计算。

 

1976 年秋，伊利诺伊大学的两位数学家阿佩尔（Appel，1932—2013）和哈肯（Haken，1928—）借助电子计算机，证明了已有100多年历史的地图四色定理，这是利用计算机解决重大数学问题的最鼓舞人心的范例。说起地图四色定理，这是由英国人提出的难得一见的著名猜想。1852年，刚刚在伦敦大学获得双学士学位的格斯里（Guthrie，1831—1899）来到一家科研单位做地图着色工作，他发现只需用4种颜色即可填满地图并使得任何两个邻国呈现不同颜色。但是，不仅他和仍然在读的弟弟无法证明这个猜想，就连他的老师摩根和哈密尔顿也无能为力。于是，凯莱经过一番研究后在伦敦数学学会做了一个报告，使得这个问题出了名。

 

►地图四色问题图例

 

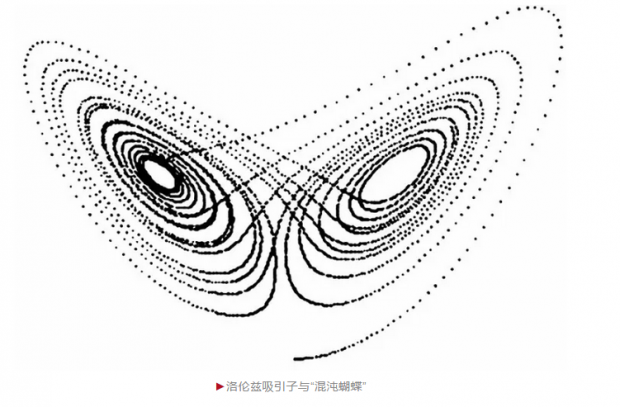
从那以后，数学家们更多地借助计算机研究纯粹数学，这方面突出的例子是孤立子（soliton）和混沌（chaos）的发现，它们是非线性科学的核心问题，可谓两朵美丽的“数学物理之花”。孤立子比四色定理出现得还早，1834年，英国工程师拉塞尔（Russell，1808—1882）在马背上跟踪观察运河中船只突然停止所激起的水波，他发现它们在行进中形状和速度没有发生明显的改变，于是称其为“孤立波”。一个多世纪以后，数学家们又发现，两个孤立波碰撞后仍是孤立波，因此被称为“孤立子”，孤立子在光纤通信、木星红斑活动、神经脉冲传导等领域大量存在。混沌理论是描述自然界不规则现象的有力工具，被视为继相对论和量子力学之后现代物理学的又一次革命。

 

计算机科学的飞速发展，不仅离不开数理逻辑，也促进了与之相关的其他数学分支的变革或创立，前者的一个例子是组合学，后者的一个典型代表是模糊数学。组合学的起源可以追溯至《易经》中的“洛书”，莱布尼茨在《论组合的艺术》中率先提出了“组合”这个概念，后来数学家们从游戏中归纳出一些新问题，如哥尼斯堡七桥问题（衍生出“图论”这一组合数学的主要分支）、欧拉36军官问题、柯克曼女生问题和哈密尔顿环球旅行问题等。20世纪下半叶以来，在计算机系统设计和信息存储、恢复中遇到的问题，为组合学研究注入了全新的强大动力。

 

相比古老的组合学，1965年诞生的模糊数学可以说是年轻的。按照经典集合的概念，每一个集合必须由确定的元素构成，元素之于集合的隶属关系是明确的，这一性质可以用特征函数μA(x)来表示：

 

 

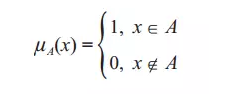
模糊数学的创始人是阿塞拜疆出生的伊朗裔美国数学家、电器工程师扎德（Zadeh，1921—），他把特征函数改写成所谓的隶属函数μA(x)：0≤μA(x)≤1，在这里A被称为模糊集合，μA(x)为隶属度。经典集合论要求μA(x)取0或1两个值，模糊集合则突破了这一限制，μA(x)=1表示百分之百隶属于A，μA(x)=0表示完全不属于A，还可以有20%隶属于A，80%隶属于A，等等。由于人脑的思维包括精确的和模糊的两个方面，因此模糊数学在人工智能系统模拟人类思维的过程中起到了重要作用，它与新型的计算机设计密切相关。但是，作为一个数学分支，模糊数学尚未成熟。

 

 

一方面，计算机的每一次飞跃都离不开数学家们的工作。另一方面，计算机的进步也推进了数学研究工作。现在，我们来谈谈几何学和计算机的奇妙结合。20世纪几何学的两次飞跃分别是从有限维到无限维（上半世纪）和从整数维到分数维（下半世纪），后者被称为分形几何学，它是新兴的科学分支——混沌理论的数学基础。拥有法国和美国双重国籍、波兰出生的数学家曼德勃罗（Mandelbrot，1924—2010）通过自相似性建立起这门全新的几何学，这是有关斑痕、麻点、破碎、扭曲、缠绕、纠结的几何学，它的维数居然可以不是整数。

 

1967 年，曼德勃罗发表了《英国的海岸线有多长？》的文章。在查阅了西班牙和葡萄牙、比利时和荷兰的百科全书后，人们发现这些国家对于它们共同边界的估计相差20%。事实上，无论是海岸线还是国境线，其长度取决于测量度的大小。一位试图从人造卫星上估计海岸线长度的观察者，相比海湾和海滩上的踏勘者，将得出较小的数值。

 

而后者相较爬过每一枚鹅卵石的蜗牛来，又会得出较小的结果。常识告诉我们，虽然这些估值一个比一个大，可是它们会趋近于某个特定的值，即海岸线的真正长度。但曼德勃罗却证明了任何海岸线在一定意义上都是无限长的，因为海湾和半岛会显露出越来越小的子海湾和子半岛。这就是所谓的自相似性，它是一种特殊的跨越不同尺度的对称性，它意味着递归，即图案之中套着图案。这个概念在西方文化中由来已久，早在17世纪，莱布尼茨就设想过一滴水中包含着整个多彩的宇宙；之后，英国诗人兼画家威廉·布莱克（Blake，1757—1827）在诗中写道：一颗沙里看出一个世界/一朵野花里有一个天堂。

 

曼德勃罗考虑了一个简单的函数f(x)=x2+c，其中x是复变量，c是复参数。从某个初始值x0开始令xn+1=f(xn)，就产生了点集{xi,i=0,1,2…}。1980年，曼德勃罗发现，对于有些参数c，迭代会在复平面的某几点之间循环反复；而对于另外一些参数c，迭代结果却毫无规律可言。前一种参数c叫吸引子，后一种叫混沌，所有吸引子的复平面子集如今被命名为“曼德勃罗集合”。

 

由于复数迭代过程即便对于较为简单的方程（动力系统）也需要海量的计算，因此分形几何学和混沌理论的研究只有借助高速计算机才能进行，结果也产生了许多精美奇妙的分形图案，不仅被用来做书籍插图，还被出版商拿去制作挂历。在实际应用中，分形几何学和混沌理论在描述和探索许许多多的不规则现象（如海岸线形状、大气运动、海洋湍流、野生生物群，乃至股票、基金价格的涨落，等等）方面，均起到十分重要的作用。

 

就美学价值而言，新的几何学赋予了硬科学特别的现代感，即追求野性、未开化、未驯养的天然情趣，这与20世纪70年代以来后现代主义艺术家所追逐的目标不谋而合。在曼德勃罗看来，令人满足的艺术没有特定的尺度，或者说它包含了一切尺寸的要素。他指出，巴黎的艺术宫殿作为摩天大楼的对立面，它的群雕和怪兽，突角和侧柱，布满旋涡花纹的拱壁和配有檐沟齿饰的飞檐，观察者从任何距离望去都能看到某种赏心悦目的细节。而当你走近时，它的构造又发生了变化，展现出新的结构元素。

 

封底推荐语

 

彭实戈，数学家

 

美是数学的一个重要特征，这一特征体现在了数学发展的整个历史进程中，但由于数学的严格性和抽象性而难以为“局外人”所体会。《数学简史》做到了这一点，作者蔡天新是我们这个世界上难得的诗人数学家。在阅读本书时体会其无处不在的诗韵本身就是一种享受，它是数学自身固有的美和作者优雅的艺术品位的巧妙融合。

 

梁小民，经济学家

 

小时候我们常把聪明的同学称为“数学脑瓜”，是指数学好才聪明。数学不仅仅是计算方法，更重要的是思维方式。我一直想推荐一本数学史，读过几本，觉得还是太专业，太难读。但这本《数学简史》我觉得任何人都会有兴趣读下去，且会有所收获。数学的发展主要在西方，但作者并没有忘记中国。更可贵的是，这本书着眼于从整个人类文明的角度来介绍数学，这就让人读起来兴趣盎然了。

 

饶 毅，生物学家

 

人类智力高低的标准是什么？一直以来有较多的争议。但数学作为人类智慧的结晶，却是长久以来达成的共识。了解数学的历史，既能了解作为高级动物的人类发展的历史，更能窥见人类智力的进步。蔡天新的《数学简史》叙述角度新颖、文字优美，让我们一起享受这本书带来的智趣吧。

►《数学简史》封面，蔡天新著，中信出版社