阅读:0
听报道
编者按:前文提到,脉冲星好似宇宙中的灯塔,发出的脉冲辐射不时地闪过人们的视线。但你或许不知道,脉冲星还是宇宙中天然的高精度时钟,每亿年误差只有1秒。
不仅如此,利用脉冲星,天文学家在上世纪七十年代首次间接地探测到了引力波,并于1993年获得与脉冲星相关的第二次诺贝尔物理学奖。
那么,脉冲星又将如何为直接探测引力波作出贡献呢?本期《天问》专栏,让我们以另一个视角,再次了解脉冲星。
撰文 | 李柯伽(北京大学)
责编 | 吕浩然
脉冲星测时
从某种意义上讲,脉冲星作为“实验室”所带来的物理探索和应用也许比脉冲星自身要丰富得多。
1993年,赫尔斯(Russell Alan Hulse)和泰勒(Joseph Hooton Taylor)因为开创了“利用脉冲星双星系统开展引力物理实验”这一领域而获得诺贝尔物理学奖,这是人类历史上首次得以研究引力波的特性来探索引力理论。而最近对使用脉冲星测时阵列直接探测引力波、脉冲星导航、脉冲星时间等热点问题的探索也正是利用脉冲星作为一个“物理实验室”而开展研究的。
脉冲星的脉冲来源于其自转(见图2动画)。脉冲星质量大约是1.4个太阳质量,而半径仅为10公里左右。由于质量大,半径小,外部的扰动就很难有效地改变脉冲星的自转特性。实际观测发现,脉冲星的转动非常稳定,特别是毫秒脉冲星的长期转动稳定性甚至比现在投入使用的国际原子钟组性能还要优良[1]。这些散布在银河系中的、转动稳定的毫秒脉冲星即构成了可以通过射电天文观测,进而可以读出“时间”的高精密时钟。其良好的时间稳定性提供了脉冲星作为基本物理实验室的基础。目前已经测得的、最精确的脉冲星每亿年误差小于1秒。
那么,射电天文观测如何去获得脉冲星时间的“读数”呢?这种技术在天文学上叫做脉冲星测时观测。它包括几个步骤:首先,人们用无线电望远镜接收脉冲星的无线电信号。为了消除色散的影响,我们需要重新对齐不同频率的脉冲信号到达地球的时间(编者注:具体方法可以参考前文)。对于较亮的脉冲星,这个时候就能够像Hewish和Bell那样看到脉冲了。
然而大部分脉冲星的信号实在是太弱了,即使消除了色散的影响,大部分情况下,脉冲信号还是不可见的。接下来让脉冲信号变得明显起来的办法叫做“周期折叠”,即按照脉冲的周期把数据分段,然后再每段数据叠加起来。这样由于将有脉冲的地方相叠加,脉冲信号就能变得明显起来。
但是仅仅获得脉冲到达地球的时间还不足以用来提取我们需要的物理信息。地球在自转,所以不同时刻,望远镜朝向天空的位置是不一样的。为了扣除地球的自转效应,我们先要计算出望远镜到地球中心的距离,把观测到的脉冲信号到达望远镜的时间归算到脉冲信号到达地心的时间。
类似地,地球还在围绕太阳作公转。因此还需要进一步计算地球相对太阳系质心的位置(太阳系质心是太阳系所有天体按照质量加权以后算出来的太阳系的“中心”),再把脉冲的达到时间归算到太阳系质心。最后,在知道脉冲星相对太阳系的运动之后,我们还要进一步把太阳系质心时间折算到相对脉冲星平动的 参考者那里(即相对脉冲星速度不变的观测者)。这样的脉冲到达时间就能表征脉冲星真实自转信息了。
脉冲星自转相当稳定。对于孤立的脉冲星来说,它的自转可以通过一个很简单的多项式模型来进行描述。测量到的脉冲时间和这个多项式模型的差异很小,但是由于测量误差和其它信号的存在,这个差异并不为零。我们把这个差异叫做“测时残差”。测时残差包含了额外的物理信息。凡是那些不在我们上述描述中的、会影响脉冲到达时间的其它所有物理过程都会在测时残差里留下踪迹。另外,如上述描述中的物理参数不够准确,那么这些信息也会留在测时残差里边。
如果脉冲星在双星系统里边,上述过程得到的是在脉冲双星质心参考者观测到的脉冲到达时间。脉冲星和伴星还在相互绕转,进一步利用双星的轨道信息,我们把脉冲到达时间再次归算到相对脉冲星平动的观测者那里。在这个过程中,通过测量脉冲星到达时间的额外变化,就能获得脉冲星伴星的信息。 例如首个系外行星系统PSR B1257+12就是这样发现的[2]。
脉冲星双星系统和太阳系看似很像,但是脉冲星双星系统的问题要复杂得多。图3描绘出了著名的脉冲双星系统B1913+16和J0737-3039A/B两个系统的轨道大小,我们按照相应比例画出了太阳的大小。可以看到,在这两个系统中,两个1.4倍太阳质量的脉冲星在与太阳大小相当的区域内作相互绕转。这样的系统由于引力很强,必须考虑广义相对论引起的效应才能得到准确的运动规律。例如,众所周知的水星轨道由于广义相对论效应引起的近星点进动量(即近星点缓慢漂移的角速度 )为每百年43角秒,而J0737则达到了每年16度!这种相对论效应明显的系统有个学名叫做“相对论性双星”,而1993年的诺贝尔物理学奖和这种双星系统密切相关。

根据广义相对论,相对论性双星系统相互绕转之时将会辐射引力波而带走系统的能量。进而致使两颗星之间的距离会相应减小,而相互绕转的频率会升高。通过脉冲星测时的方法,测量脉冲双星的轨道周期随时间变化的规律,再同广义相对论引力波带走能量而预言的轨道周期变化进行比较,即可检验广义相对论是否正确。
在上世纪六十年代初期,科学界认为引力波探测是一项不可能完成的任务。然而脉冲双星系统B1913+16的发现及其轨道周期变化的测量[3]间接地证明了引力波的存在、引力波会带走能量,同时也证明了引力波带走能量的方式与广义相对论预言一致。不过,通过脉冲双星对引力波的测量仍是间接测量,因为我们测量的是脉冲星轨道周期的变化,进而推断出系统能量的减少,再而证明引力波存在的。所以脉冲星双星实验是间接推断了“引力波的存在”。或多或少受脉冲双星工作的影响,到了上世纪七十年代, 科学界部份敏锐的研究人员已经意识到引力波探测也许不是遥不可及得了。
截至目前,双星系统对引力波的间接测量和引力检验的精度比上世纪七十年代已经高了不少,目前测量值和广义相对论预言的偏差小于0.1%[4]。
脉冲星测时阵列
现在让我们从引力波的间接探测回到脉冲星测时问题。根据前文介绍的内容,我们已经知道了三件事情:一、脉冲星会发出非常准确的周期性脉冲信号;二、我们能够利用望远镜来读出脉冲到达地球的时间;三、测时残差(即脉冲星到达时间的模型和测量的区别)包含了其它的物理信息。
那么哪些物理信息能够被我们观测到呢?我们又怎么提取这些信号?我们将通过两个前沿的应用例子给予说明:脉冲星时间-空间标准及引力波直接探测。
脉冲星时间-空间标准
目前我们用的时间是从1972年1月1日开始通行的国际协调时(UTC)。它是用原子钟定义的时间加上地球自转观测修正构成的。
那么,国际协调时是如何确定的呢?首先,人们通过加权平均地球上运行的大约500个原子钟的时间构成国际原子时(TAI)。在这个基础上,人们再通过闰秒修正获得国际协调时。在应用国际协调时的时候,因为每个原子钟的数据无法实时进行汇总,人们并不能实时地获得加权时间。精确时间测量仍然需要进行事后改正。
如果我们在脉冲星测时观测过程中没有考虑国际原子时的变化的话,那么脉冲星计时残差里边就会留下相应的信号。反过来,如果国际原子时本身有误差的话,那么我们也应当能够从脉冲计时残差里边看到这个误差。问题在于,每颗脉冲星也有自己的不稳定性,我们如何区分测时残差究竟是来源于脉冲星自身的不稳定性,还是来自国际原子时的误差呢?读者也许会自然而然地想到:我们同时观测了多颗脉冲星。
如果没有“阴谋论”的原因的话,可以预计,每颗脉冲星的自转特性是完全独立的,一颗脉冲星自转变化的时候,不会影响其它脉冲星的自转变化。所以如果测时残差来源于脉冲星自身,那么每颗星的变化应该是不一样的。但是如果测时残差来源于国际原子时的不稳定性,情况就不一样了。
不妨假设由于某些原因,国际原子时提前了一秒。那么我们用这个国际原子时作为基准去测量脉冲星的脉冲到达时间,将会观察到所有脉冲星的到达时间都推迟了一秒钟,也即所有脉冲星的测时残差都会出现一秒的跳变。按照这个讨论,如果我们把脉冲星测时残差中公共的那部分提取出来,那么这部分信号就可以认为是国际原子时的系统误差。如能进一步再利用这个信号,对国际原子时进行修正,即完成了脉冲星钟和国际原子时之间的校正[5]。这种对多颗脉冲星进行测时观测并综合起来分析处理的技术叫做脉冲星测时阵列。
除了时间标准,我们还能够利用脉冲星建立空间框架。我们已经知道,在进行脉冲星测时观测的时候需要准确地知道地球在太阳系中的位置。如果我们对这个知识掌握的不够准确,那么就会有可观测的误差。因此我们可以在数据中搜寻太阳系中未知的小行星,或者对一些参数非常不确定的系统(例如第九大行星)进行限制[6]。在X射线波段也能看到脉冲星。利用类似的技术,可以测量X射线卫星的位置[7],即实现X射线卫星的脉冲星导航。
这种方式适合深空探测。因为在远离地球的地方,传统的GPS卫星定位或者干涉定位精度会逐渐变差,而使用脉冲星则可以在从太阳系到整个银河系的尺度上构造基本的时间和空间框架。不过地面设备支撑仍然必不可少,因为还需要知道地球相对于这个框架的坐标。
脉冲星测时阵列直接探测引力波
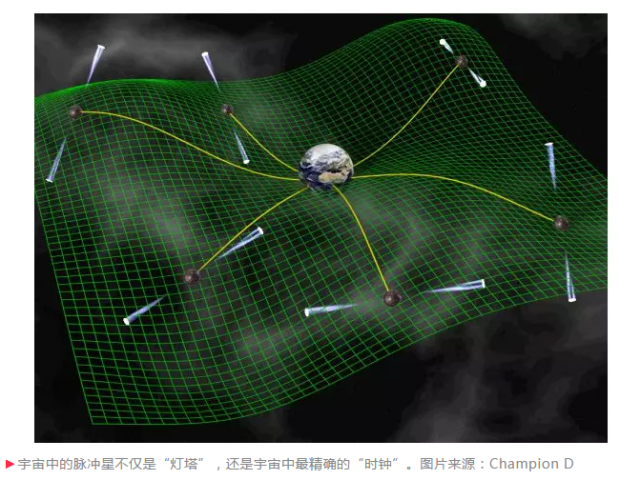
脉冲星测时阵列还能够直接探测引力波。这里脉冲星被当成了标准的脉冲信号发生器来使用,其发出的脉冲信号穿过银河系的距离来到地球。如果宇宙背景中存在引力波,就会改变银河系的时空结构,从而改变信号的到达时间(参见图4)。
广义相对论预言,引力波是时空的涟漪,而且是“横波模式”。这也就是说,在垂直于波传播方向上的空间被拉伸或者压缩。同时引力波还具有一种特性,叫做“无迹”。这并不是说引力波不留下痕迹,而是指引力波压缩空间某个方向的时候,同时会拉伸相应的垂直方向(图4中的水平和垂直方向)。这样自由观测者围成的空间体积近似不变。
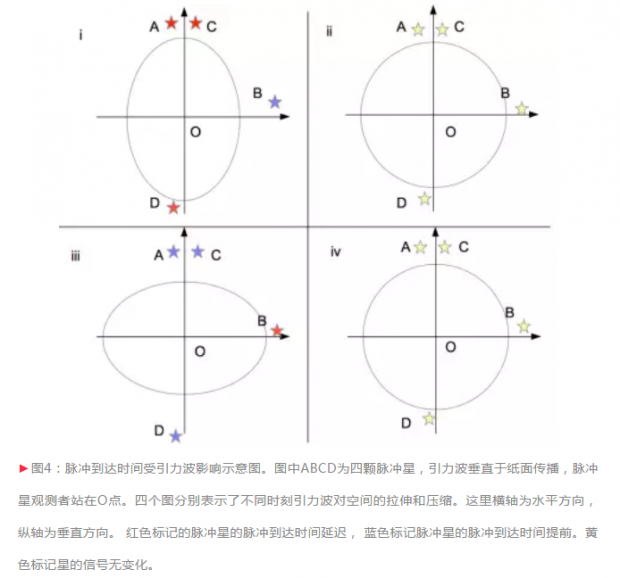
这种时空的拉伸和压缩会导致在相应方向上“距离”的改变,从而使得脉冲到达地球的时间提早或者延迟(严格来说,在弯曲时空中,谈论空间两点的距离意义并不明确,我们这里的“距离”按照观测者测量的光之到达时间来理解)。
按照图4的示意。由于引力波的“无迹”性,两颗处于垂直位置的脉冲星(图中A和B)的脉冲信号具有“相反”的特点,也就是一颗星的脉冲到达地球如果变早了,那么另外一颗星的脉冲到达地球时间就会推迟。类似的推理不难得知,两颗位置相似的脉冲星(图中A和C)的脉冲信号是同相的(即两颗星的信号同时延迟或者提前);而位置相反的两颗脉冲星(图中A和D)脉冲信号也是同相的。
数学上有一种描述信号同相或相反的运算,叫做相关运算。完全一致的信号,计算出来的相关系数为1;如果是完全反相的信号,则计算出来的系数为-1。细致的计算表明:来自宇宙四面八方的引力波背景会导致每对脉冲星的信号都变得有相关性,而且这个相关性和脉冲星的之间的角距离是有关系的。
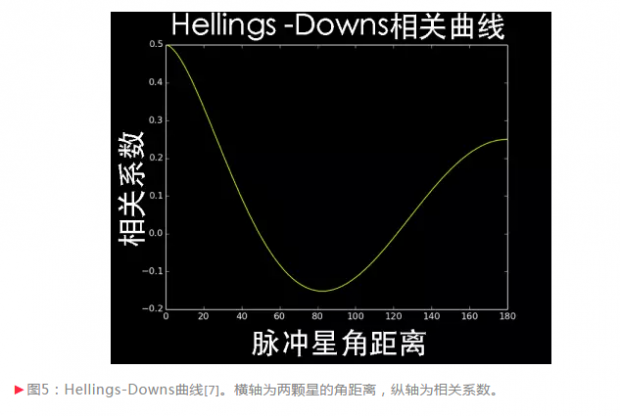
图5则画出了这个角度依赖的关系。这个关系是1983年由Ronald Hellings和George Downs发现的[8]。图中这条曲线因此也称为Hellings-Downs曲线。我们把脉冲星测时残差拿过来,做相关计算,如果能够探测到Hellings-Downs曲线,我们就测量到引力波了。
那么脉冲星测时阵列能够探测哪些引力波呢?我们又是否值得去进行这项实验?引力波的类型很广,不同频率的引力波观测的对象也不一样,能够探索的科学目标非常不同。脉冲星测时阵列的特点决定了它能够探测的引力波是极低频的纳赫兹(相应周期大约为10年 )引力波;反过来,在纳赫兹波段里,脉冲星测时阵列是唯一的探测手段。
纳赫兹引力波的周期长达数年。目前我们已知的宇宙中,这种引力波来源于星系中心的亿到万亿倍太阳质量的超大质量黑洞相互绕转及并合,宇宙弦及宇宙早期暴涨的残余引力波的高频部分。而地面激光干涉仪LIGO探测的引力波则在百赫兹到千赫兹的高频波段。探测的对象是恒星级相对论性天体并合事件。
由于这些天体的质量较小,因此探测距离不是很远。脉冲星测时阵列针对的是星系中心的超大质量双黑洞并合过程,由于星系级黑洞的并合对于宇宙结构形成和演化起着主导的作用,这些引力波源的探测则直接打开了探索宇宙结构的引力波窗口。
除了频段,脉冲星测时阵列和激光干涉仪还有另外一个区别。地面激光干涉仪的仪器尺度大约为几公里,而探测的引力波波长为数百公里。脉冲星测时阵列则是一个银河系尺度的引力波探测器,其仪器尺度由脉冲星到地球之间的距离决定,可以有几千光年的大小,而相应探测的引力波波长大约为光年量级。由于测不准原理的限制,如果仪器尺度小于待测信号的波长,那么仪器必然无法获得很好的定位能力。反过来,如果仪器尺度大于波长,那么就有希望进行高空间分辨率的探测。
类似的例子是耳朵和眼睛。眼睛之所以能够看得清楚,就是因为眼睛的尺度远远大于光波长可以具备高的空间分辨率。耳朵无法成像,是因为耳朵的物理尺度小于声波波长,无法提供高的空间分辨率。事实上,LIGO的空间分辨率的确不佳,而脉冲星测时阵列可以直接进行引力波成像观测[9]。
读者可以看到,我们这里讨论的脉冲星测时阵列探测引力波和之前提到的利用双星的周期变化间接证明引力波存在非常不一样。脉冲星测时阵列探测引力波是直接探测引力波的手段。脉冲星测时阵列探测引力波的原理是检测不同脉冲星到达时间的相位差。这与利用激光干涉仪探测引力波原理一样。只不过激光干涉仪测量的是不同光路的激光的相位差,脉冲星测时阵列中,我们测量了脉冲星到达时间的相位差。
目前国际上有大型射电天文望远镜的国家联合起来组成了国际脉冲星测时阵列合作项目(参见图6)。其中包括欧洲的EPTA,澳大利亚的PPTA,以及美国的NANOGRAV。他们分别依托欧洲5个100米级望远镜(Effelsberg, Jodrell Bank, Nançay, WSRT和Sardinia)、澳大利亚Parkes望远镜、美国Green Bank和Arecibo望远镜等国际上几个口径最大的望远镜展开工作。
目前,国际脉冲星测时阵列的灵敏度已经逼近了做出“发现”的水平,极有可能在几年之内成功地探测到纳赫兹波段的引力波。

我国现已建成了世界上最大的500米单口径望远镜FAST,新疆在建世界最大的全可动高频110米口径望远镜QTT(奇台望远镜),还有可能建造世界最大的干涉阵列ChinaART。这些望远镜由于具有很大的接收面积,可以有效提高脉冲星测时的精度。可以预计,如果这些望远镜能够及早完成调试并投入使用,则脉冲星测时阵列探测引力波的领域将有重大的突破。
*作者注:感谢研究生郭彦君、胥恒、张春风和李洋阅读本文的初稿,但文责由作者自负。
作者简介:
· 李柯伽,2003年获北京大学天文系学士学位,后获得博士学位(2009),随后进入马克思-普朗克射电天文研究所从事博士后研究。现为北京大学科维理天文与天体物理研究所研究员。主要研究领域:脉冲星、引力波、快速射电暴、射电天文技术与方法和统计信号探测理论。
参考文献:
1.Hartnett G.J., and Luiten N.A., Comparison of astrophysical and terrestrial frequency standards. Review of Modern Physics, 81(2011):1.
2.Wolszczan, A. and Frail, D. (1992). A planetary system around the millisecond pulsar PSR1257 + 12. Nature. 355 (6356): 145
3.Taylor, J.H., Fowler, L.A., and McCulloch, P.M., Measurements of general relativistic effects in the binary pulsar PSR1913+16. Nature, 277(1978):437.
4.KramerM., etal., Strong-field tests of gravity with the double pulsar. Annalender Physik, 518(2006):34.
5.HobbsG., etal., Development of apulsar-basedtime-scale. Monthly Notices of the Royal Astronomical Society, 427(2012):2780.
6.GuoJ. Y., LeeJ.K., & Caballero N.R., A dynamical approachin exploring the unknown mass in the Solar system using pulsar timing arrays. Monthly Notices of the Royal Astronomical Society, 475(2018):3644.
7.Downs S.G., and Reichley E.P., Techniques for measuring arrivaltimes of pulsar signals 1: DSN observations from 1968 to 1980. California Institute of Technology, Jet Propulsion Laboratory. Pasadena:NASA,(1980)
8.Hellings W.R., and Downs S.G. Upper limits on the isotropic gravitational radiation background from pulsar timinganalysis. Astrophysical Journal, 625(1983):39.
9.LeeK .J., etal., Gravitational wave astronomy of singles ources with a pulsar timingarray. Monthly Notices of the Royal Astronomical Society, 414(2011):3251.

话题:
0
推荐
财新博客版权声明:财新博客所发布文章及图片之版权属博主本人及/或相关权利人所有,未经博主及/或相关权利人单独授权,任何网站、平面媒体不得予以转载。财新网对相关媒体的网站信息内容转载授权并不包括财新博客的文章及图片。博客文章均为作者个人观点,不代表财新网的立场和观点。




 京公网安备 11010502034662号
京公网安备 11010502034662号 