赌徒谬误：赌博与大数定律-知识分子的财新博客-财新网

撰文 | 张天蓉（美国德州大学奥斯汀分校理论物理博士）

责编 | 吕浩然

概率论专栏

2017-03-16 上帝教人掷骰子——“神童”帕斯卡与概率论

2017-03-31 似是而非的答案：概率论悖论

2017-04-18 别相信直觉：概率论帮助侦破“财务造假”

●　●　●

先讲一个赌场捞金的故事。

很多人都听说过概率或统计中的蒙特卡罗（Monte-Carlo）方法，是一种在统计的基础上利用大量数据进行计算的方法。这其中的蒙特卡罗指的并不是人名，而是摩纳哥一个著名赌场的名字。自蒙特卡罗赌场于1865年开张后，摩纳哥从一个穷乡僻壤的弹丸之地，一跃成为欧洲最富有的国度之一，至今已经150年过去，这个国家仍然是以赌场和相关的旅游业为主。

约瑟夫•贾格尔（Jagger）[1]是约克郡一个棉花工厂的工程师，在工作之余经常光顾蒙特卡罗赌场，尤其对前文提到的轮盘游戏特别感兴趣。他认为，轮盘机器在理想的情况下，每个数字出现的概率都是1/38。但是，机器怎么可能做到完美对称呢？任何缺陷都可以改变获奖号码的随机性，导致转盘停止的位置偏向某些数字，使这些数字更为频繁地出现。那么，赌徒应该可以利用这种偏向性来赚钱！

1873年，贾格尔下决心要改变自己的命运：他带上所有的积蓄来到蒙特卡罗赌场，并雇用了六个助手，每个助手把守一个轮盘机器。白天，他们记录每个轮盘的所有数据；晚上，贾格尔便在旅馆里独自分析这些数据中的规律。六天后，前五个轮盘的数据并没有发现有意义的偏离，但第六个轮盘为贾格尔带来了惊喜：38个数字中有9个数字出现的概率要比其余的频繁得多！贾格尔兴奋不已，第七天他前往赌场，认定了那台有偏向性的轮盘，大量投注这九个高概率的数字，当天就赚了7万。虽然后来赌场改变了策略，却让贾格尔获取了一笔不菲的收入。

贾格尔是幸运的，但更多的赌徒却是十赌九输。主要原因有两个：一方面是因为所有赌场游戏的概率设计本来就是以利于赌场为准，这样赌场才能稳赚不赔；另一方面，利用赌徒的心态也是赌博游戏设计者们的拿手好戏。赌徒谬误便是一种常见的、不符合概率规则的错误心态，经常被赌场利用。

赌徒谬误（The Gambler's Fallacy）

赌徒谬误大意是指将前后相互独立的随机事件当成有关联的事件，例如抛硬币时，无论抛几次，任意两次之间都是相互独立的，并不相互产生影响。

道理虽简单易懂，但有时仍会糊涂。比如，当你连抛了5次正面时，到了第6次，你可能会认为这次正面出现的概率会更小了（< 1/2），反面出现的概率会更大（> 1/2）。也有人会逆向思维，认为既然5次都是1，也可能继续是1（也被称为热手谬误）。实际上，这两种想法都掉进了“赌徒谬误”的坑。也就是说，将独立事件当成了互相关联事件。

赌徒有了“赌徒谬误”的心态，会输得更惨。比如说，赌场中著名的输后加倍下注系统（Martingale）便是利用此心态的实例：赌徒第一次下注1元，如输了则下注2元，再输则变成4元，如此类推，直到赢出为止。赌徒误以为在连续输了多次之后，胜出的概率会变大，所以愿意加倍又加倍地下注，殊不知其实概率是不变的，赌场的游戏机没有记忆，不会因为你输了就给你更多胜出的机会。

赌徒谬误不仅见于赌徒，也经常反映在一般人的思维方式中。中国人常说“风水轮流转”，这句话在很多时候或许反映了现实，但如果将这种习惯性的思维方法随意地应用到前后互相独立的随机事件上，便会跌入赌徒谬误之中。

对“大数定律”的误解

赌徒谬误产生的另一个原因是对“大数定律”的误解。

大数定律[2]指的是当随机事件发生的次数足够多时，发生的频率趋近于预期的概率。

对一枚对称硬币而言，正面的预期概率是1/2。当我们进行n次实验后，得到正面出现的次数n正，比值p正 = n正/n，叫做正面出现的频率，此时p正不一定等于正面出现的概率（1/2）。但是，当n逐渐增大时，频率将会逐渐趋近1/2。也就是说，频率取决于多次实验的结果，而概率则是一个极限值，实验次数越大，频率越趋近概率，这就是大数定律。

提出并证明了大数定律最早形式的是瑞士数学家雅各布•伯努利（Jakob Bernoulli ,1654－1705），雅各布也是概率论的重要奠基人之一。直到他死后的第8年，即1713年，大数定律才在《猜度术》（Ars conjectandi）中得以呈现，这本巨著也使概率论真正成为数学的一个分支，其中的大数定律和以后将会提到的由狄莫弗（A.de Moivre）和拉普拉斯（P.S.Laplace）导出的“中心极限定理”，是概率论中极其重要的两个极限定理。

赌徒们对大数定律的误解主要体现在对“多次重复”的理解。多少次试验才算“足够多”，才能到达大数定律能够实用的大样本区间？此问题的答案：理论上是无穷大，实际中难以定论。大多数情形是：还没到“足够多”，该赌徒便已经财力耗尽、赌注输光、两手空空了！

有人喜欢买彩票，并且在每次填写彩票时，要选择以往中奖号码中出现少的数字，还振振有词地说这样做的依据是大数定律：某个数字过去出现得少，以后就会多，为什么呢？“要满足大数定律啊！”，可见对大数定律误解之深。

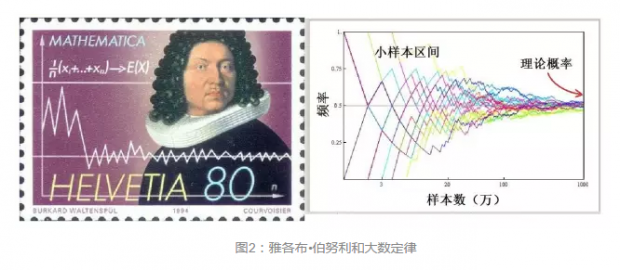
而对赌徒思维误区的专业解释，便是将大数定律应用于试验的小样本区间，将小样本中某事件的概率分布看成是总体分布，以为少数样本与大样本区间具有同样的期望值，把短期频率当成长期概率，或把无限的情况当成有限的情况来分析。实际上，这是在错误应用大数定律时的心理偏差，因此被心理学家卡尼曼和特维尔斯基戏称为“小数法则”。事实上，任何一段有限次的试验得到的频率对于足够多次的试验的频率几乎没有什么影响，大数定律说的是总频率趋近于概率值，如图2b所示，小样本区间试验的结果并不影响最后趋近的概率。

圣彼得堡悖论

与雅各布•伯努利同属伯努利家族的尼古拉•伯努利（Nikolaus I. Bernoulli，1687年－1759年）也是一名热衷研究赌博的数学家，他提出了著名的“圣彼得堡悖论”。为了理解这个悖论，首先从赌博游戏的期望值说起。

赌博的输赢与期望值有关，期望值是以概率为权重的平均值。赌博的方式不一样，“赢”的期望值也不一样。以38个数字的轮盘为例，按照一般赌场的规矩，赌注押在其中一个数字上，如果押中，顾客得到$35，否则损失$1的赌注。顾客赢钱为正，损失为负，则顾客“赢钱”的期望值公式为：

E（顾客“赢”的期望值）= - 输钱数*输钱概率+赢钱数*赢钱概率

第一项是负值，表示是顾客“输”掉的钱数。

由此而计算出上述假设条件下的期望值E= -1*37/38+35*1/38=-0.5。

可以看到，期望值是负数，对赌徒不利。但设想有个傻一点的赌场老板，将上面规则中的“赢钱数”$35改成$38的话，算出的期望值就会成为正数，这种策略就对顾客有利了，赌徒们高兴了，将蜂拥而至。如果将$35改成$37呢？这时候算出来的期望值为0，意味着长远来说，赌徒和赌场打平了，双方不输不赢（不计开赌场的费用），称之为“公平交易”。

因此，期望值也是那些“理性赌徒”们决定“赌或不赌”的数学依据。

然而，根据这个数学依据作出的决策有时候完全不符合人们从经验和直觉所作的判断。这是怎么回事呢？尼古拉•伯努利便以“圣彼得堡悖论”为例对此提出质疑[4]。

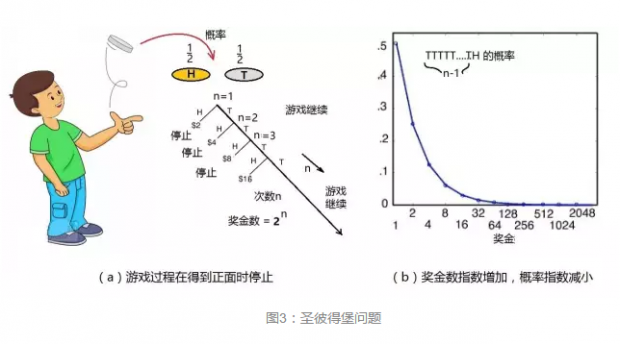
尼古拉设想了一种简单的游戏方案：顾客不需要每次下赌金，但得买一张价钱固定（m元）的门票参加，游戏规则如下：

顾客只是掷（公平）硬币，掷出正面就停止，掷出反面就继续掷，直到掷出正面为止，见图3a。如果游戏停止了，顾客就能得到奖金，奖金的数目与掷的次数有关。游戏持续次数越高，奖金就越高。比如说，游戏停止时掷了n次，那么顾客可得奖金数为（2n）元。

叙述得更具体一点：如果第一次掷出正面，游戏停止，顾客只能得2元（21），若掷出反面，就继续掷。若第二次掷出正面，顾客得4元（22），若掷出反面，又继续掷……依次类推，顾客若一直得到反面直到第n次才掷出正面，奖金数便是（2n）元，奖金数随n增大而指数增加。

现在，计算这个游戏中，顾客“赢钱”的期望值，即每次期望赢得的钱乘以概率后相加。然后，再将m元的门票作为负数放进去，得到期望值是：

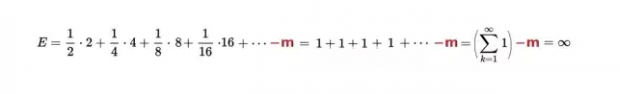
从以上计算可见，无论门票m是多少（有限数），得到的期望值都是无穷大！这很诡异，因为“期望值无穷大”意味着无论收多高的门票，赌徒都会赢！这就出现了矛盾，因此，尼古拉认为这是一个悖论，人们在做决策的时候，并不仅仅考虑数学期望的大小，更多的是在考虑风险。数学期望值不能完全描述风险。

为什么叫“圣彼得堡悖论”呢？因为这个悖论被尼古拉提出却是被其堂弟丹尼尔•伯努利解决的，丹尼尔提出经济学中的效用理论来解释这个问题，论文发表在1738年圣彼得堡召开的一次学术会议上，所以得名为圣彼得堡悖论[5]。

赌博虽然是一种恶习，由它却引发了不少有趣的数学问题，促进了概率论的发展，由于圣彼得堡悖论的解决而建立了“效用理论”，推动了经济学的发展。概率论中除了大数定律之外，还有一个极其重要的“中心极限定理”，有关中心极限定理极其应用，是我们下一篇的内容。

参考资料：

[1] Wikipedia：Men who broke the bank at Monte Carlo

https://en.wikipedia.org/wiki/Men_who_broke_the_bank_at_Monte_Carlo

[2] 维基百科：大数定律

https://zh.wikipedia.org/wiki/%E5%A4%A7%E6%95%B0%E5%AE%9A%E5%BE%8B

[3] The Bernoulli Family, by H. Bernhard, Doubleday, Page & Company(1938) .

[4] "The St. Petersburg Paradox", The Stanford Encyclopedia of Philosophy

https://plato.stanford.edu/archives/fall2004/entries/paradox-stpetersburg/

[5] Bernoulli, Daniel: 1738, "Exposition of a New Theory on the Measurement of Risk", Econometrica 22 (1954), 23-36.

话题：