►图片来源：pixabay 

 

前面两篇中所介绍的大数定律和中心极限定理，都是基于多次实验结果的经典概率观点，属于概率论中的频率学派。事实上，概率和统计中还有另一个极端的派别——贝叶斯学派。两派的争论焦点涉及到“什么是概率？概率从何而来？”等本质问题。

 

撰文 | 张天蓉

责编 | 吕浩然

 

●　●　●

 

历史回顾

 

托马斯·贝叶斯（Thomas Bayes， 1702－1761）虽为英国的一位古人，却在当代科技界“红”了起来，原因归结于我们曾经在第二篇中介绍过的贝叶斯定理。这个定理现在被广泛应用于与人工智能密切相关的机器学习中。

 

当年，贝叶斯研究过“白球黑球”的概率问题。概率问题可以正向计算，也能反推回去。下面举正向计算的例子，比如，暗盒里有10个球，黑白两种颜色。如果我们知道10个球中5白5黑，那么，如果我问你，从中随机取出一个球，这个球是黑球的概率是多大？问题不难回答，当然是50%！如果10个球是6白4黑呢？取出一个球为黑的概率应该是40%。

 

再考虑复杂一点的情形：如果10个球中2白8黑，现在随机取2个球，得到1黑1白的概率是多少呢？10个球取出2个的可能性总数为10*9=90种，1黑1白的情况有16种，所求概率为16/90，约等于17.5%。因此，只需进行一些简单的排列组合运算，我们便可以在10个球的各种分布情形下，计算取出n个球，其中m个是黑球的概率。这些都是正向计算。

 

不过，贝叶斯当时更感兴趣的是反过来的问题（可称之为逆概率问题）：假设我们预先并不知道盒子里黑球白球数目的比例，只知道总共是10个球，那么，如果我随机地拿出3个球，发现是2黑1白。是否可以通过这个试验样本（2黑1白），猜测盒子里白球黑球的比例呢？这就是逆概率问题。

 

可以从最简单的抛硬币试验来说明“逆概率”问题。假设我们不知道硬币是不是两面“公平”的，也就是说，不了解这枚硬币的物理偏向性，这时候，得到正面的概率p不一定等于50%。那么，逆概率问题便是企图从某个（或数个）试验样本来猜测p的数值。

 

为了解决逆概率问题，贝叶斯在他的论文中提供了一种方法，即贝叶斯定理：

 

后验概率 = 观测数据决定的调整因子×先验概率

 

上述公式的意义，指的是对未知概率首先有一个“先验”猜测，然后结合观测数据，修正先验，得到更为合理的“后验”概率。“先验”和“后验”是相对而言的，前一次算出的后验概率，可作为下一次的先验概率，与新的观察数据相结合，再得到新的后验概率。因此，运用贝叶斯公式，有可能对某种未知的不确定性逐次修正概率模型并得到最终结果，即解决逆概率问题。

 

有关贝叶斯定理的论文，直到贝叶斯死后的1763年，才由朋友代为发表。后来，拉普拉斯（Pierre-Simon Laplace,1749-1827）证明了贝叶斯定理的更普遍的版本，并将之用于天体力学和医学统计中。

 

频率学派和贝叶斯学派：客观主观之争

 

也许贝叶斯当初对他自己这个定理的意义认识不足，恐怕也没有料到由此可以启发人们以一种全新的思考方式来看待概率和统计，并继而发展成所谓的“贝叶斯学派”【1，2】。

 

贝叶斯学派，是相对于“频率学派”而言的，二者更像是一种哲学争论。频率学派将概率定义为事件多次重复后发生的频率之极限。但是，这只是代表我们使用概率这个名词的某一种情况。很多时候，概率无法通过多次试验来得到，比如说，今天北京下雨的概率，或者，加州某年某月某日地震的概率，这些是无法用多次重复来验证的。再比如说，某个国家研制的导弹，命中1000公里外目标的概率，理论上可以重复，但事实上并不会用多次重复来得到这个概率，因为花费太昂贵了。

 

从上面所举的几个实例可见，概率一词所描述的是对“不确定性” 的度量。这种度量既有客观因素，也有主观因素。有时候，不确定性是物体的固有属性，是独立于主观因素的客观存在。比如硬币或骰子，它的物理偏向性如何？某一面出现的概率是多少？是否“公平”？这些都是在物体的制造过程中决定了的，原则上可用频率派多次实验的方法来探索它的概率。但在某些情形，“不确定性”的客观意义并不显而易见，例如在清华对北大的某次篮球赛中，某人预言清华队“赢”的概率，是他的个人观点结合两个球队实力得出的主观猜测，这时候，使用贝叶斯定理逐次更新概率模型的方法更为合适。

 

那么，概率到底是客观的，还是主观的？这便涉及到了“概率之本质”的哲学问题，因此，频率派和贝叶斯派的争论焦点实际上是哲学意义上的。如果仅就科学研究的意义上，两个学派的统计学家基本上都承认大数定律和中心极限定理，也都使用贝叶斯公式，只是两派使用这些定理的方式和场合不完全一样，各有利弊而已。

 

英国数学家及哲学家弗兰克·拉姆齐（Frank Ramsey，1903-1930）在他1926年的论文中首次建议将主观置信度作为概率的一种解释，他认为这种解释可以作为频率解释的一个补充或代替。

 

概率有时候是主观的，比如以赛马为例，大多数观众并不具备对马匹和骑师等因素的全面知识，而只是凭主观因素对赛马结果下赌注，他们认可的某个马匹的获胜概率反映的是他们的个人信念，因而是主观概率。

 

科学有别于哲学，尽管物理世界是客观存在的，解决问题的科学方法却总是人为的，难免掺进主观的因素，自觉或不自觉地，明显的或隐含的。不管哪个派别，主观性都在所难免。作为数学的应用，必须具体问题具体分析，哪种方法有效便使用哪一种，主观还是客观之说法，只不过是凌驾于科学之上的“哲人”们对理论的不同诠释，对解决具体问题无济于事。

 

频率派强调概率的客观性，一般用随机事件发生的频率极限来描述概率；而贝叶斯派则将对不确定性的主观置信度作为概率的一种解释，并认为：根据新的信息，可以通过贝叶斯公式不断地导出或者更新现有的置信度。

 

在历史上，贝叶斯统计长期受到排斥，受到当时主流的数学家们的拒绝。然而，随着科学的进步，贝叶斯统计在实际应用上取得的成功慢慢改变了人们的观点。贝叶斯统计慢慢地受到人们的重视，人们认为它的思路更为符合科学研究的过程以及人脑的思维模式。目前贝叶斯概率已经成为一个热门研究课题，在机器学习中大展宏图，在物理学中也有应用。以下简单介绍量子力学诠释中的“量贝模型”，看看贝叶斯方法如何启发人们从不同的视角来思考问题。

 

量子贝叶斯模型

 

尽管量子力学在应用方面已经取得了巨大的成就，但人们一直被种种诡异的量子现象所困扰，即使在顶尖物理学家之间，也难以达成共识，可谓众说纷纭。其中主流派的观点，也就是大多数教科书上的解释，被称之为“哥本哈根诠释”。

 

量子理论与经典理论的不同之处以及哥本哈根诠释，都可以借助“薛定谔的猫”来理解。

 

从日常生活经验，一只猫要么死，要么活，不可能“既死又活”。但量子力学相关的实验结果却告诉我们，微观粒子的状态似乎是“死活”并存的（即波粒二象性），但我们又无法探索这种状态的详情，因为一旦实施测量，便没有了既死又活的猫，结果只看到死猫或活猫。于是，哥本哈根诠释解释说：在进行测量之前，粒子的波函数为叠加态，一旦进行测量，便干预了量子态，发生“波函数塌缩”，按照一定的概率塌缩到“死”“活”状态之一。塌缩概率可根据波函数的平方来计算，这种特殊的叠加态及塌缩，便是量子力学奇妙现象之根源，但哥本哈根诠释并未真正解决“既死又活”的薛定谔猫的量子悖论。更多有关量子及量子纠缠的内容，请参考笔者在科学网和《物理》的系列文章【3】。

 

贝叶斯派的主观概率思想与量子力学的哥本哈根诠释在某些方面有异曲同工之妙，因此，在本世纪初，有三位学者发表了一篇题为《作为贝叶斯概率的量子概率》的短论文【4】，探索一种量子力学的新诠释。三人都是经验丰富的量子信息理论专家，他们将量子理论与贝叶斯派的概率观点结合起来，建立了“量子贝叶斯模型”，或简称为“量贝模型”（QBism）。

 

量贝模型与哥本哈根诠释有关，但又有所不同。哥本哈根诠释认为波函数是客观存在，人为的“测量”干扰并破环了这个客观存在，使得量子叠加态“塌缩”，从而造成悖论。量贝模型则认为波函数并非客观实在，只是观察者所使用的数学工具。波函数不存在，也就没有什么“量子叠加态”，如此便能避免诠释所产生的悖论。

 

根据量子贝叶斯模型的诠释，概率的发生并不是由物质的内在结构决定的，而是与观察者对量子系统不确定性的置信度有关。他们将与概率有关的波函数定义为某种主观信念，观察者得到新的信息之后，根据贝叶斯定理的数学法则得到后验概率，不断地修正观察者本人的主观信念。

 

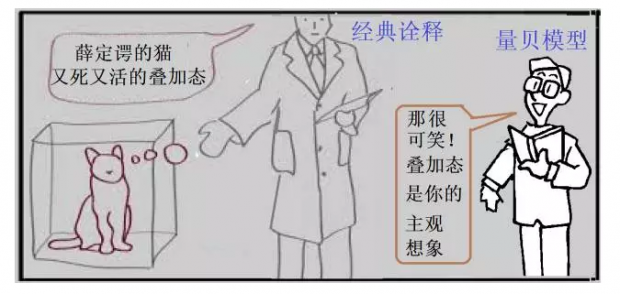
量贝模型认为：波函数是主观的，但量子系统却是独立于观察者而客观存在的。每个观察者使用不同测量技术，修正他们的主观概率，对量子世界作出判定。在观察者测量的过程中，真实的量子系统并不会发生奇怪的变化，变化的只是观察者选定的波函数。对同样的量子系统，不同观察者可能得出全然不同的结论。观察者彼此交流，修正各自的波函数来解释新获得的知识，于是，就逐步对该量子系统有了更全面的认识。这也是贝叶斯方法的思维方式。

 

根据量贝模型，盒子里的“薛定谔猫”并没有处于什么“既死又活”的恐怖状态。但盒子外的观察者对里面的“猫态”认识不够，不足以准确确定它的“死活”，便主观想象它处于一种死活二者并存的叠加态，并使用波函数的数学工具来描述和更新观察者自己的这种主观信念。

 

举一个通俗例子来说明此类主观想像的“叠加态”。在2016年美国总统大选中，特朗普和希拉里都有“胜败”的可能性，但结果难以预测。对某个特朗普的支持者而言，在不知道特朗普最后到底是“胜”还是“败”之前，只能凭着他个人的主观置信度来估计特朗普“胜败”概率（比如52%：48%），这就像认为特朗普是处于某种“胜败”并存的叠加态中。这种叠加态的概率分配是这个人主观的，其他人可能会有不同概率分配的主观叠加态。

 

量贝模型创建者希望能用概率论来重新构建量子力学的标准理论。这个目标尚未达成，结论如何，还需拭目以待。但贝叶斯方法为量子诠释提供了一种新视角【5】。之后介绍机器学习时，还将更详细讨论贝叶斯方法，下一篇将着重介绍随机过程。

 

参考文献：

【1】维基百科：贝叶斯概率

https://zh.wikipedia.org/wiki/%E8%B4%9D%E5%8F%B6%E6%96%AF%E6%A6%82%E7%8E%87

【2】Edwin Thompson Jaynes. Probability Theory: The Logic of Science. Cambridge University Press, (2003).

【3】张天蓉. 走近量子纠缠系列之三：量子纠缠态[J]. 物理, 2014, 43(09): 627-630.

http://www.wuli.ac.cn/CN/abstract/abstract61515.shtml

【4】C. M. Caves, C. A. Fuchs and R. Schack, “Quantum Probabilities as Bayesian Probabilities,” Phys. Rev. A65, 022305 (2002).

【5】Hans Christian Von Baeyer，QBism: The Future of Quantum Physics，Harvard University Press，10/3/2016。