撰文 | 施    郁（复旦大学物理学系教授）

 ● ● ●

全文分十一章：

1.    1918至1919年的规范理论

2.    量子论拯救规范理论

3.    规范理论的重生

4.    克莱因和泡利

5.    杨-米尔斯理论

6.    粒子物理标准模型与杨-米尔斯理论的复兴

7.     实验给杨-米尔斯理论赋予生命

8.     诺贝尔奖获奖演讲中的杨-米尔斯理论

9.     对称性支配相互作用

   10.    规范理论与数学

   11.    规范理论的美与真

1918年至1919年，位于苏黎世的瑞士联邦工业大学的赫尔曼·外尔（Hermann Weyl）发表了三篇文章，试图将电磁力纳入引力几何理论的框架 [1-4]。这就是规范理论的开端。外尔是20世纪最有影响的数学家之一。曾获得有“数学诺奖”之称的菲尔兹奖和阿贝尔奖的迈克尔·阿蒂亚（Michael Atiyah）爵士曾经告诉笔者，外尔是他的偶像之一。

赫尔曼· 外尔。图源：wikipedia

外尔的这三篇文章，以《引力与电》（Gravitation and electricity）一文为主，该文发表于《普鲁士科学院院刊》[2]。正是在这个杂志上，爱因斯坦1915年发表了引力的几何理论，也就是广义相对论，揭示了引力本质上是物质所导致的时空的弯曲 [5]。  

1905年，爱因斯坦提出狭义相对论。闵科夫斯基注意到，狭义相对论将时间和空间统一为四维时空。十年以后，爱因斯坦的广义相对论指出，物质使得时空弯曲，弯曲时空又决定物质的运动。

为了领会时空弯曲的含义，让我们想象一个球面。在球面上的某一点放一个箭头，箭头从这一点指向某个方向。然后我们将箭头的底端在球面上移动，移动过程的每一个瞬间，都保持箭头方向不变，这叫平行移动。然而，对于有限长度（非无穷小）的移动，箭头方向却变了。为了方便比较，我们可以让箭头底端沿着某个闭合曲线平行移动一圈，回到原来的位置，箭头的方向不再是原来的方向。这就是球面弯曲所导致的。在弯曲时空里，道理与此类似，任何一个矢量（既有大小也有方向，就像一个箭头）的平行移动可能改变它的方向，但是大小不变。

当时人们了解到，自然界有两种基本力，除了引力，就是电磁力，由电磁势决定。所以外尔自然地想将电磁力也纳入广义相对论的框架。他试图推广平行移动的观念，构想矢量平行移动时，不仅方向变化，大小也变化。对于无穷小的平行移动，矢量大小改变无穷小倍，外尔假设这个无穷小倍数正比于电磁势的无穷小改变。不难推导出，对于一个有限长度的平行移动，矢量大小就变成原来的大小乘以一个指数因子，指数正比于电磁势沿着路径的积分（也就是将每一点的电磁势累加）。这个改变矢量大小的指数因子依赖于平行移动所经过的路径，所以叫做不可积标度因子。

这个结论很奇怪。在相对论里，尺子大小和时钟快慢都可以看成矢量的大小。那么按照外尔的理论，两点之间的尺子大小和时钟快慢的改变居然取决于尺子和时钟沿什么路径移动！

这就是爱因斯坦在外尔《引力与电》一文后所作评论的内容。评论后面还发表了外尔篇幅很长但是没有说服力的答复，但是他承认自己“像野鹅一样追逐疯狂的概念”。

在外尔的这篇文章中，有一句话体现了外尔的思考方式（本文中的直接引文均为作者译自英文）：

可以看出，外尔的信心源于他提出电磁守恒定律背后的不变性，或者说对称性。这里的守恒量并非今天我们所知的电荷（那需要修正后的规范理论）。外尔这里将对称性导致的守恒量与能量动量守恒相比较。这些都可以当成诺特定理的例子。诺特定理是说，对称性对应于守恒量。不知外尔当时是否已经知道也发表于1918年的诺特定理 [6]。当时诺特在哥廷根大学希尔伯特的麾下，但是五年前外尔就已经离开了。

量子论出现以后，1922年，外尔的朋友薛定谔猜测，可以在外尔的标度因子的指数里加上虚数单位i [7]。这样，标度因子就成了一个大小为1的复数，也就是量子力学波函数的相位因子。但是薛定谔当时还没有波函数的概念，只是笼统地说某个“长度”。后来人们发现，这个工作对薛定谔1926年创立波动力学起了启发作用 [8-10]。

也是在1922年，在经典理论中，卡鲁扎（Theodor Kaluza）将4维时空推广到5维时空，其中某些度规分量代表电磁势（度规是指两点坐标与它们之间距离的关系）。当理论不依赖于第5维坐标时，5维坐标变换退化为4维坐标变换和1维规范变换。

1926年，薛定谔通过4篇文章创立了量子力学的波动力学表述（因此分享1933年诺贝尔物理学奖）。他在第4篇文章中指出，电磁场中带电粒子的动量和能量算符必须包含电磁势 [11]。量子力学里，物理量要用算符表示，意思是对波函数进行运算。

同样是在1926年，克莱因（Oskar Klein）和福克（Vladimir Fock）分别讨论了卡鲁扎理论对应的波动力学 [12,13]。福克特别指出，波函数运动方程具有规范不变性，就是说，将波函数乘以相位因子，同时电磁势做一个相应的变换，运动方程依然成立 [13]。

1926年底，伦敦（Fritz London）写了一封信给薛定谔，询问他1922年对规范因子的修改与他1926年波动力学的联系 [8-10]。然后伦敦自己写了两篇文章，将通常的波动力学与外尔的规范理论联系起来，将外尔的不可积标度因子改为波函数的不可积相位因子[14-15]。伦敦的工作没有福克的5维理论的额外负担。

在伦敦和福克工作的铺垫基础上，外尔在1928年的《量子力学中的群论》一书 [16]和1929年的两篇文章中 [17-18]，终于修正了他1918至1919年的理论，正式将标度因子改为相位因子，将标度不变性改为相位不变性，但是沿用了原来的名词“规范（eich）”。我们特意将他在1918年1919年间的不可积因子称作标度因子，因为标度因子和相位因子都称作规范因子。2019年恰好也是规范理论重生九十周年。   

1929年的这两篇文章是外尔以美国普林斯顿大学访问教授的身份完成的。第一篇是发表于《美国科学院院刊》（PNAS）的英文概要《引力与电子》（Gravitation and the electron），里面出现了“规范不变原理”（principle of gauge invariance）。第二篇是德文文章，内容详尽，标题是《电子与引力》（Elektronund gravitation）。两个标题与他1918年的《引力与电》（Gravitation and electricity）颇为呼应。

规范不变原理当然就是外尔1929年文章中最重要的内容。在量子力学框架下，电磁学作为规范不变的后果被推导出来，规范不变性还导致电荷守恒。这里的规范变换已经不是一个实数的标度因子，而是相位因子（指数上有个虚数单位），规范不变性事实上是相位不变性。这就是我们今天熟悉的规范理论。

导致电荷守恒的规范不变是在整体规范变换（又称第一类规范变换）下，也就是相位变换与时空坐标无关，对每时每地的波函数作同样的相位变换。这可以看成诺特定理的例子，虽然外尔没有直接提到诺特定理。1929年，诺特定理已经广为人知。而导出电磁学的规范不变性是在局域规范变换（又称第二类规范变换）下，也就是说，相位因子依赖于时空坐标。

外尔1929年的文章仍然将引力和电磁力通盘考虑，但是现在需要考虑量子力学，出发点是引力场中的电子自旋。因此外尔讨论了二分量旋量理论（用两个波函数描述电子），包括具有手征性的外尔旋量（后来被称为外尔费米子）。

笔者发现特别有趣的是，在外尔的理论中，局域平直时空依赖于时空坐标，从而导致了一种联络，与时空弯曲的克里斯托弗联络相加，类似于后来人们所知的非阿贝尔规范势，而相应的黎曼张量类似于非阿贝尔规范场场强！

被誉为“物理学的良心”和“上帝的鞭子”的量子力学创始人之一泡利（Wolfgang Pauli，因泡利不相容原理独享1945年诺贝尔物理学奖）写了一封信给外尔 [19-20]：

泡利。图源：wikipedia

外尔这篇文章引起泡利的反感是可以理解的：外尔1918年的文章是带着爱因斯坦的质疑一起发表的，泡利当年也反对 [4]，现在居然卷土重来，再加上文章里面的二分量理论是违反宇称守恒的（宇称守恒等效于镜面对称）。后来，1933年，泡利在他著名的《物理学手册》的文章里仍然批评二分量理论。1957年1月，泡利听说吴健雄等人关于弱相互作用中宇称不守恒的实验后（弱相互作用是主宰粒子衰变的基本相互作用），先是表示不相信宇称不守恒，十天后读了论文，才改变看法。  

但是泡利看了外尔1929年第二篇规范理论的文章后，态度完全变了，又写了一封信 [19-20]：

1930年，外尔去哥廷根大学任教，成为他的导师希尔伯特的继任者。

泡利成了规范理论的支持者。在上面所说的他1933年《物理学手册》文章中，也介绍了外尔的规范理论 [21]。

也是在1933年，外尔收到普林斯顿高等研究院的教授聘书，他没有接受。后来德国政治局势恶化，他接受了普林斯顿高等研究院再次相聘。他在那里工作到1951年退休，后来在苏黎世和普林斯顿两地生活，以苏黎世为主。

虽然经典电磁学中也讨论规范和规范变换，但是这个名词的使用是在1929年外尔用量子力学修改规范理论之后 [22]。

质子和中子统称为核子，通过强核力结合成原子核。1922年，考虑到强核力与每个核子是质子还是中子无关，海森堡提出同位旋的概念，类似于自旋，将质子和中子表示成同位旋的两种基本状态，而在强核力下，同位旋守恒。1936年，汤川秀树提出强核力的介子理论，即核子之间通过交换介子而产生强核力，正如带电粒子之间的电磁力通过交换光子而实现。光子没有质量，所以电磁力是长程的，但是介子是有质量的，所以强核力只能局限于很短的距离。

数学上，外尔的规范变换属于U(1)变换，只有1个波函数作一个相位变换。而核子的同位旋变换属于SU(2)变换，对应于两个同位旋状态的2个波函数作满足一定条件的变换。对于某种变换而言，如果连续作两次变换的结果与顺序无关，就叫阿贝尔的，否则就叫非阿贝尔的。U(1)变换是阿贝尔的，SU(2)变换是非阿贝尔的。

1938年，克莱因在波兰的一个会议上提出一个包含引力、电磁力和强核力的统一理论[20,23]，将上面提到的卡鲁扎-克莱因理论中对第5维坐标的无关性改为依赖于某个相位因子，其中第5维坐标出现在指数上。这个新理论中，某些度规系数成为具有SU(2)非阿贝尔规范结构的矩阵。克莱因将此理论用于核子。克莱因并不要求该理论具有SU(2)规范不变性。不过他评论说质量项可能不需要，质量也许可以来自某种自能，这个猜想有点后来的希格斯机制的精神。克莱因的报告没有引起与会者多少兴趣，后来又只是发表在会议文集，再加上二战的爆发，这个工作没有引起关注。

1953年在莱顿召开的洛伦兹-昂内斯会议上，普林斯顿高等研究院的派斯（Abraham Pais）为了研究粒子分类，提出一个基于同位旋的场论，将每个时空点推广为一个2维球面，试图将外尔的电荷守恒推广到同位旋守恒 [20,24]。派斯只考虑了整体规范变换，也就是说，SU(2)变换与时空坐标无关。泡利在场，他评论道 [20,24]：

泡利是在问，能否将与时空坐标无关的同位旋SU(2)整体变换改为依赖时空坐标的SU(2)局域规范变换。他自己立即研究了这个问题。泡利熟悉规范理论，以前也研究过引力和电磁力的统一理论 [24]，也赞成外尔将电子旋量理论与引力理论结合起来。

在1953年7月和12月给派斯的两封信中，泡利描述了自己的理论，题为“介子-核子相互作用与微分几何”（Meson-nucleon interaction and differential geometry） [20,24,25]。他也用卡鲁扎-克莱因理论，但是采用了两个额外维度。在他的理论中，电磁势不是来自度规，而是来自克里斯托弗联络。泡利在这里没有写下规范场的拉格朗日量以及场方程，也没有正式发表这个理论。但他在1953年秋天做过相关演讲，后来他的学生整理了讲义 [24]。1954年泡利在给杨振宁的一封长信中说，他的学生在这个讲义里讨论了规范场的拉格朗日量 [26]。1953年12月，泡利给派斯的另一封信中说 [24]：

着重标志是泡利本人所加。这里以及后来泡利与杨振宁的对话以及给杨振宁的长信反映出，泡利意识到规范粒子的质量是个麻烦。这是因为如果规范粒子有质量，理论的规范不变性也就失去了；而如果规范粒子没有质量，就意味着规范场可以将作用力传递无限远，但是这与强核力的情况不符。

杨振宁当时是普林斯顿高等研究院的年轻成员，是派斯的同事，但是1953年夏至1954年夏，他在布鲁克海文实验室访问。杨振宁曾经回忆 [27]：

杨振宁接着回忆，在芝加哥读研究生时，他就开始尝试将规范理论推广到同位旋。2005年出版的《杨-米尔斯理论50年》（50 Years of Yang-Mills Theory）收入了杨振宁在1947年的三页笔记 [28]，编者特霍夫特（Gerardus ’t Hooft）说 “这是一个当时在为规范不变性概念而努力的研究生的笔记，距1954年的杰作还有一段长路。” 1947年后杨振宁还进行了很多不成功的计算。

后来随着实验上越来越多的介子被发现，杨振宁认为需要一个写下相互作用的原理。所以1953年夏天在布鲁克海文实验室，杨振宁回到这个问题。当时，他与即将在哥伦比亚大学博士毕业的米尔斯（Robert Mills）共用一个办公室。这一次，两人终于完成了规范理论的非阿贝尔推广 [27]。

杨振宁和米尔斯。图片来源：《杨振宁选集》

1954年2月，杨振宁回到普林斯顿高等研究院作学术报告，介绍这个理论 [27]。泡利在听众中，那个时期他与老朋友外尔一样在苏黎世与普林斯顿高等研究院之间“振荡”。犀利的泡利不断问杨振宁规范粒子的质量。杨振宁回答说不知道，曾经研究过，但是没有明确结论。泡利说：“这不是充分的理由。”第二天，杨振宁收到泡利的短信，去找泡利。泡利建议杨振宁去看薛定谔关于引力场中狄拉克方程的文章。杨振宁发现，里面的方程一方面与黎曼几何有关，一方面与他和米尔斯的方程类似 [27]。这个月，泡利还写了一封长信给杨振宁，将自己之前的结果在平直时空和其他条件下简化，与杨-米尔斯的结果一致，并说他的学生讨论了规范场的拉格朗日。泡利最后写道 [26]：

杨振宁和米尔斯的工作与广义相对论完全无关，没有额外维度的负担。在他们的文章之前，除了伦敦的文章和泡利的综述，研究不可积规范因子和规范理论的论文都将规范场与引力纠缠在一起，这有一定误导性，但有一定技术上的优势。杨振宁和米尔斯在明确的物理动机下，提出清晰的非阿贝尔规范理论。但是因为他们当时不了解规范场的几何意义，不知道场强可以直接从协变导数的对易子得到。而克莱因和泡利的工作是在弯曲时空理论的框架中，所以很自然地通过协变导数的对易子得到场强。不过笔者注意到，在泡利当初介绍外尔规范场的综述文章中，对于通常的平直空间，也用协变导数的对易子表示了场强 [21]。杨振宁没有留意到这一点，否则推广的过程会顺利很多。

尽管受到泡利的批评，杨振宁依然认为想法很美，应该发表。这体现了巨大的勇气，因为泡利的批评有强大的杀伤力。比如1925年，乌伦贝克（George Uhlenbeck）和哥德斯密特（Samuel Gouldsmit）提出电子具有自旋。这个贡献没有得到诺贝尔奖，因为克罗尼格（Ralph Kronig）大半年前提出同样想法，但在泡利、海森堡和克雷默斯（Hendrik Kramers）反对下没有发表。

2012年，杨振宁说 [29]：

1954年，杨振宁和米尔斯其实发表了两篇文章，提出杨-米尔斯理论。第一篇只是杨振宁在当年美国物理学会四月会议所作报告《同位旋守恒与推广的规范不变性》（Isotopic spin conservation and a generalized gauge invariance）的摘要，发表在《物理评论》（Physical Review），很好地总结了杨-米尔斯理论的物理思想 [30]：

他们另一篇文章是详细的论文《同位旋守恒与同位旋规范不变性》（Conservation of isotopic spin and isotopic gauge invariance），于6月28日被《物理评论》收稿。此文的摘要强调了局域变换 [31]：

文章最后说明，对于规范粒子的质量问题，还没有满意答案，并指出质量为零的选项面临发散的困难。

我们顺便提一下，整体对称也是合法的，不与规范对称矛盾，两种对称都存在，前者也可看成后者的特例，事实上电荷守恒正是整体相位变换不变性的后果。

虽然是一个很美的理论，但是杨-米尔斯理论没有能立即用到物理上。当时除了在普林斯顿，杨振宁只在哈佛大学作过一次介绍这个工作的演讲。

2012年，杨振宁评论 [32]：

这里提到的[85j]就是杨振宁的《外尔对物理学的贡献》[4]，里面的脚注34指出，泡利生前最后一些年对规范场的思想持负面态度，并提到1956年泡利曾经为他1921年的文章《相对论》写过一系列后记，其中关于“外尔的理论”的后记不再如他1921年的德文原文那样正面。

总之，杨振宁和米尔斯成为非阿贝尔规范理论的创立者，非阿贝尔规范理论也被称为杨-米尔斯理论。1999年，在美国物理学会成立100周年之际，杨振宁当初的同事和见证人派斯写了理论粒子物理的历史综述，其中写道 [33]：

杨-米尔斯理论的发表使得很多物理学家开始关注这个问题，成为一个候选理论，虽然并没有立即成功解决具体物理问题。杨振宁回忆：“1950年代后期，规范理论被用到强相互作用和弱相互作用。1960年，樱井（Jun John Sakurai）发表了一篇很热切的文章，提出强相互作用的非阿贝尔规范理论。” [27] 但是杨振宁认为樱井的做法破坏了规范不变性这一规范理论中最美妙的观念，认为不应当马马虎虎地将规范理论变为唯象的东西[34]。1961年，格拉肖 (S. Glashow) 如樱井一样，硬行假设规范粒子具有质量，提出一个具有U(1)× SU(2)对称性的模型，以统一电磁相互作用和弱相互作用。

另一方面，杨-米尔斯理论也引起一些纯理论的兴趣。1960年代，费曼（R.P.Feynman）、德维特（B. DeWitt）、波波夫（V. N. Popov）和法捷耶夫（L. D. Faddeev）研究了杨-米尔斯理论的量子化。

后来，经过其他很多物理学家多年的努力，在加入其他思想元素之后，杨-米尔斯理论成为粒子物理标准模型的理论架构。描述的对象有别于1954年时的设想。质子和中子不再是基本粒子，同位旋守恒只是近似的。轻子和夸克是基本粒子。核子由夸克组成，核子之间的强核力来自夸克和胶子的强相互作用。基本相互作用包括强相互作用以及统一了电磁和弱相互作用的“电弱相互作用”，它们分别由一个杨-米尔斯理论描述。

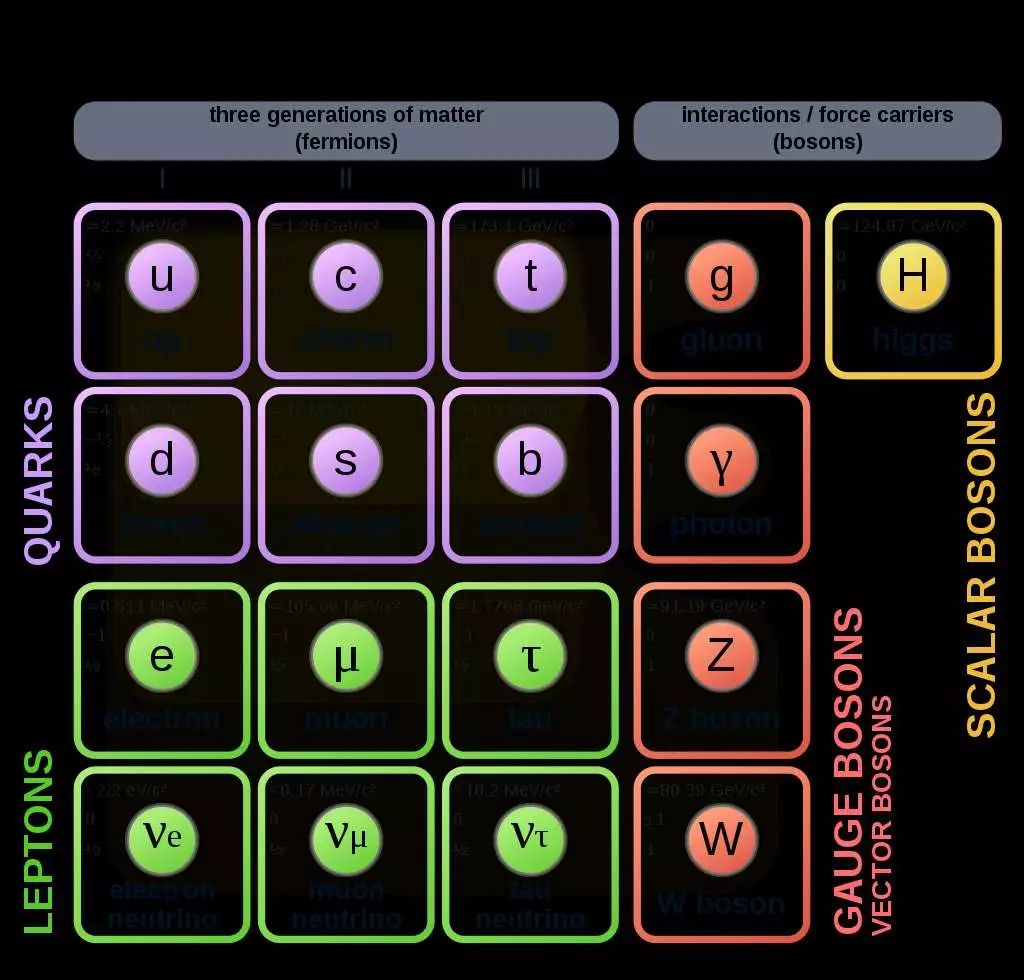
粒子物理标准模型。来源：wikipedia

除了规范对称性，粒子物理标准模型的另一个主要思想是自发对称破缺。这个思想最早出现在凝聚态物理中，特别是超导理论中，1960年由南部阳一郎（Yoichiro Nambu）首先引入粒子物理。他指出，真空不一定具有能量函数的对称性。

1963年，安德森（P. W. Anderson）借鉴超导理论，指出规范对称的自发破缺会导致规范粒子获得质量。1964年，布劳特（R. Brout）和英格莱特（F. Englert），希格斯（P. W. Higgs），以及稍后的古拉尼克 (G. Guralnik)、海根 (C. R. Hagen) 和基堡（T. Kibble）三组研究者指出，在相对论场论中，规范对称的自发破缺使得规范粒子获得质量。这个机制也导致有质量的希格斯粒子的产生。正如杨振宁曾经评价的那样 [34]：

1967年，基于规范对称的自发破缺，作为轻子的模型，温伯格提出具有U(1)×SU(2)规范对称性的电弱理论。萨拉姆在一个会议上也独立提出这个理论，并首次采用“电弱理论”之名[35]。自发对称破缺使得电弱作用的规范粒子（带1个正或负的单位电荷的W±和不带电的Z0粒子）获得质量，理论此后的部分与格拉肖1961年建立在人为假设基础上的理论一致。1971年，温伯格又将此理论用于夸克。1971年至1972年，特霍夫特和维尔特曼（M. Veltman）证明了杨-米尔斯理论的可重整化,这是一个重大突破，表明了电弱理论是一个自洽的量子场论。

粒子物理标准模型还有一个主要思想是所谓的渐进自由。1973年，格罗斯（David Gross）和韦尔切克（Frank Wilczek）,以及普利策（David Politzer）发现杨-米尔斯理论具有渐进自由的性质，也就是说，距离越短，相互作用越弱。特霍夫特在前一年得到这个结果，但是没有发表。渐进自由的发现确定了量子色动力学的物理意义。这是弗里兹希（H. Frizsch）和盖尔曼（M. Gell-Mann）1972年提出的、具有SU（3）规范对称性的杨-米尔斯理论，通过被称作色的自由度描述强相互作用，其规范粒子就是胶子。在SU(3)变换中，3个波函数作符合一定条件的变换。后来，格罗斯和韦尔切克以及温伯格提出，量子色动力学的规范对称没有破缺，因此胶子质量为零。轻子和希格斯粒子无色，因此不参与强相互作用。

1972年，小林诚（Makoto Kobayashi）与益川敏英（Toshihide Maskawa）在电弱理论框架中，提出一个3代共6种（这个种类叫做味）夸克微弱混合的模型，解释实验上观测到的弱相互作用的CP对称性破坏（这里的对称性破坏不是前面谈的自发破缺）。C指电荷共轭，就是在数学上将粒子变换为它的反粒子，P指宇称变换，CP指同时作着两个变换。1956年，李政道和杨振宁的理论分析表明，弱相互作用中宇称是否守恒有待实验检验，然后吴健雄通过钴60的β衰变实验，发现弱相互作用中P和C都是不对称的，李和杨因此获得1957年诺贝尔物理学奖。1964年，克罗宁（James Cronin）和费奇（Val Fitch）在中性K介子的衰变中发现，CP也是不对称的，他们因此获得1980年诺贝尔物理学奖。   

1974年，威尔逊（Kenneth Geddes Wilson）发明了格点规范场论，通过将时空分立化，进行非微扰的计算。他1982年因为用重整化群研究相变获得诺贝尔物理学奖。

1970年左右，杨振宁认识到规范场的几何意义和不可积相位因子的重要性。他1974年发表了规范理论的积分形式，并提出引力就是一种规范场 [36]。1975年，杨振宁和吴大峻用不可积相位因子给出规范场的整体描述，并将规范理论与纤维丛理论的基本概念相对应 [37]，促进了数学与物理学此后在这方面的成功合作。在此背景下，1985年和1987年，杨振宁在外尔和薛定谔的百年诞辰纪念会上讨论了相关的历史 [4,9]。

外尔从规范不变性得到电磁理论，窥视到大自然理论结构的一角，但是电磁理论早就从大量实验中被物理学家总结出来，由麦克斯韦集大成。杨-米尔斯理论能否成为描述基本相互作用的理论框架、标准模型正确与否都需要接受实验的检验，因此实验给杨-米尔斯理论赋予了生命。实验上的验证也给很多为建立标准模型作出重要贡献的物理学家带来诺贝尔物理学奖。

当初杨振宁和米尔斯的工作就受到实验上发现大量介子的驱动。介子先是在宇宙线中发现，1953年布鲁克海文实验室的质子同步加速器 COSMOTRON 投入运行后也发现很多介子。杨-米尔斯理论在提出后受到质疑,则是由于理论中的规范粒子当时在实验上不存在。

1970年代，电弱理论预言的中性流在欧洲核研究组织（CERN）、费米实验室和斯坦福直线加速器实验室（SLAC）的很多实验中得到证实，因此，格拉肖、萨拉姆和温伯格分享了1979年的诺贝尔物理学奖。

格拉肖（Glashow）、萨拉姆（Salam）、温伯格（Weinberg）。

图源：http://www.boiledbeans.net

1983年，电弱理论中的规范粒子W±和Z0粒子在CERN被发现，因此鲁比亚（Carlo Rubbia）和范德米尔（Simon Van der Meer）分享了次年的诺贝尔物理学奖。W±、Z0乃至其他粒子具体性质的计算（包括1995年才在费米实验室发现的顶夸克的质量）依赖于特霍夫特和维尔特曼的规范场重整化理论，因此他们“因澄清电弱理论的量子结果”而分享了1999年的诺贝尔物理学奖 [38]。  

实验表明夸克不能孤立存在，只有在高能量时才能观测到，所以需要一个具有渐进自由性质的强相互作用理论。格罗斯和韦尔切克以及普利策的计算表明杨-米尔斯理论具有这样的性质，他们分享了2004年的诺贝尔物理学奖。量子色动力学经受了很多实验的检验，比如，用粲夸克及其反粒子的束缚态解释J/ψ粒子的行为，预言电子-质子深度非弹性散射偏离比约肯（James Bjorken）标度并得到实验证实，以及对夸克喷注现象的解释。1968年，费曼曾用部分子模型解释比约肯标度，部分子很快被认为就是夸克 [39]。

南部阳一郎与小林诚（Kobayashi Makoto）和益川敏英（Toshihide Maskawa）的工作都使得规范对称框架下的标准模型能够解释不对称的实验事实，因此他们分享了2008年的诺贝尔物理学奖。1972年，小林诚和益川敏英的模型提出来的时候，只有3种已知的夸克。1964年比约肯和格拉肖曾提出第4种夸克，称为粲夸克。1970年，格拉肖、伊利波洛斯（Jean Iliopoulos）和玛雅尼（Luciano Maiani）用电弱理论表明，粲夸克的存在可以解释在弱相互作用下，奇异数的改变不超过1。1974年，丁肇中组和里希特（B.Richter）组发现J/ψ粒子，确认了粲夸克的存在乃至夸克模型的真实性，被称为“十一月革命”。丁肇中和里希特分享了1976年诺贝尔物理学奖。1977年，伯尔（Martin Perl）组发现τ轻子（伯尔分享了1995年诺贝尔物理学奖），表明轻子有3代，莱德曼（Leon Lederman）组发现第5种夸克。这样，小林诚和益川敏英的模型开始得到重视。第6种夸克就是1995年才发现的顶夸克。

2012年， CERN发现了希格斯粒子，次年英格莱特和希格斯分享了诺贝尔物理学奖（布劳特已于2011年去世）。

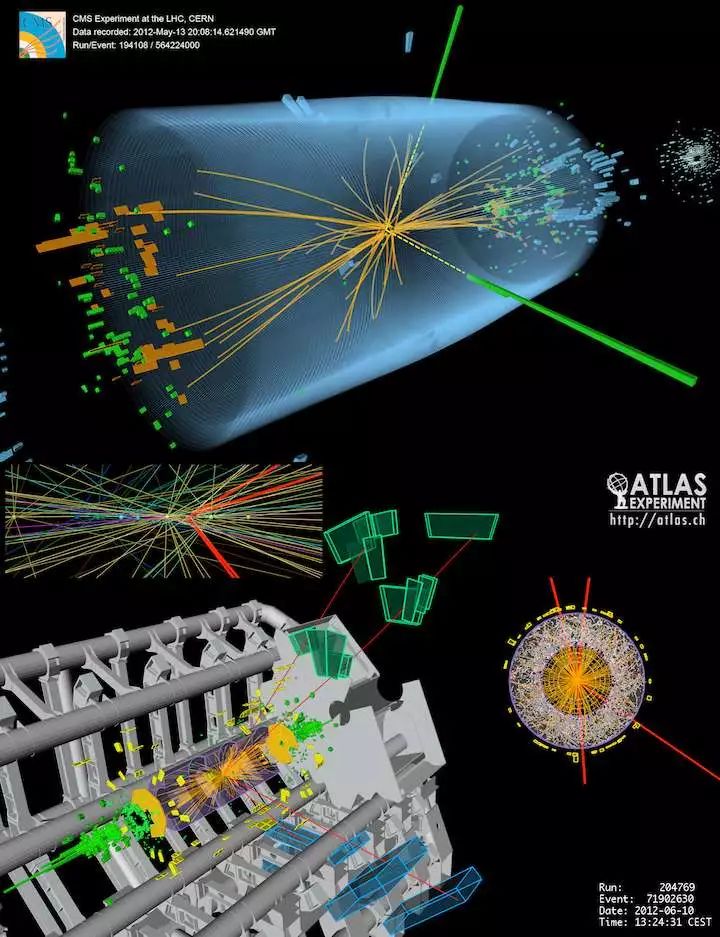
希格斯粒子的实验发现。来源：wikipedia

很多相关诺贝尔物理学奖获奖演讲中，都提到杨-米尔斯理论或者非阿贝尔规范理论 [38]。笔者在“杨-米尔斯理论60周年”国际会议上曾将这些片段集中展示 [40]，它们足以描绘一段精彩纷呈的历史。

格拉肖（1979年获奖）：

温伯格（1979年获奖）：

维尔特曼（1999年获奖）：

特霍夫特 (1999年获奖):

格罗斯（2004年获奖）：

南部阳一郎（2008年获奖）：

小林诚 (2008年获奖):

益川敏英 (2008年获奖):

英格莱特（2013年获奖）：

希格斯（2013年获奖）：

1955年12月，外尔在苏黎世去世。此前不久，外尔将1918年的《引力与电》收入他的文集，并写了个评论 [20]：

这里外尔提到了规范不变性与电荷守恒的对应关系。这在他1918年的文章里没有，但是在他1929年的文章以及泡利对规范不变性的介绍中都提到了，当时已经广为人知。

将外尔的此段总结与杨振宁和米尔斯文章的摘要相对照，更显有趣。用规范原理导出电磁学是在已经了解电磁学规律之后，只是厘清理论结构，但是正如坐标变换不变性决定了未知的引力，非阿贝尔规范不变性决定了未知的规范相互作用。

1979年，在纪念爱因斯坦诞辰100周年的一个会议上，杨振宁总结了“对称性支配相互作用”原理，指出第一个例子是爱因斯坦从坐标变换不变性得到广义相对论，第二个例子是外尔从阿贝尔规范变换不变性得到电磁学，第三个例子是从非阿贝尔规范变换不变性得到非阿贝尔规范场 [41]。今年也是“对称性支配相互作用”这一概括提出40周年。

在纪念外尔百年诞辰的演讲中，杨振宁说 [4]：

戴森 (Freenman J. Dyson) 在普林斯顿高等研究院度过漫长的事业生涯，与外尔和杨振宁都很熟悉，是杨-米尔斯理论的另一位见证人。戴森曾经说 [42]：  

戴森继续评论道：

2002年，杨振宁总结20世纪理论物理的三个主旋律：量子化，对称和相位因子[43,44]。

杨振宁先生曾经告诉笔者：

“对称性支配相互作用”的三个例子体现了物理学理论之大美。另一方面，这三个例子又都体现了理论物理与数学的密切关系。广义相对论对应的数学黎曼几何（弯曲空间的几何）在十九世纪上半叶就由高斯（Karl Friedrich Gauss）和黎曼（Bernhard Riemann）师徒创立，然后里奇（Gregorio Ricci）和乐维-齐维塔（Tullio Levi-Civita）师徒发明了张量微积分这个分析黎曼几何的工具。爱因斯坦开始创立广义相对论时，他的同学格罗斯曼（Marcel Grossmann）告诉他，合适的数学就是黎曼几何。

关于规范理论的数学，杨振宁曾经写道 [41]：

阿蒂亚曾经写道 [45]：

在杨振宁和吴大峻1975年的《不可积相位因子概念和规范场的整体形式》中 [37]，有一个“字典”，把规范理论的基本概念“翻译”成纤维丛理论的基本概念。其中，规范理论中的源对应一个问号，因为当时数学家还没有研究与源对应的概念。无源情况的一种解是自对偶解，又叫瞬子解，这是只有单个奇点的极小作用量解，由贝拉凡（A. Belavin）、普利亚科夫（A. Polyakov）、施瓦茨（A. Schwartz）和图普金（Y. Tyupkin）首先得到。

阿蒂亚与合作者研究了瞬子解的分类。他与希钦（Nigel Hitchin）和辛格合作，运用阿蒂亚-辛格指标定理（两人因此获得2004年阿贝尔奖），计算了瞬子模空间的维数。

阿蒂亚关于杨-米尔斯与规范理论的一个系列学术报告激发了凯伦·柯斯库拉·乌伦贝克（Karen Keskulla Uhlenbeck，Keskulla是婚前姓，她第一个丈夫的父亲就是自旋提出者之一乌伦贝克）对规范理论的兴趣。她将杨-米尔斯方程表示成一个椭圆系统，导致她所谓“曲率受限于Lp的联络”的紧致定理，以及“被戳破的4维球上的杨-米尔斯方程的可去除奇点”的理论。她还证明，任何具有有限作用量和孤立奇点的解处于一个SU(2)纤维丛上。陶布斯（Clifford Taubes）研究了瞬子模空间的边界和自对偶4维流形的粘结。

在阿蒂亚、凯伦·乌伦贝克和陶布斯等人工作基础上，唐纳森（Simon Donaldson）用瞬子模空间研究了4维微分流形的拓扑，得到了唐纳森定理，并与费里德曼（Freedman）定理结合，发现4维欧氏空间上存在奇异微分结构，由此获得1986年菲尔兹奖。凯伦·乌伦贝克和丘成桐发现，复n维流形上的稳定全纯矢量丛上存在厄密杨-米尔斯联络。

威腾（Edward Witten）用规范场论（特别是超对称杨-米尔斯理论）研究低维拓扑等数学问题，他是唯一获得过菲尔兹奖的物理学家（因为证明了广义相对论中的正能量定理）。这说明广义相对论和规范理论都能反哺数学。

关于杨-米尔斯理论的数学，凯伦·乌伦贝克有过一段有趣的评论 [46]：

本文排版期间（2019年3月19日），“因为对几何偏微分方程，规范理论和可积系统的开创性贡献，以及在分析，几何和数学物理上的基本影响”，凯伦·乌伦贝克获2019年阿贝尔奖 [47]。

外尔曾经半开玩笑地对戴森说 [42]：

外尔对规范对称的执着深刻地反映了这一点。所幸，规范对称是美的，也是真的。安德森曾经说过 [48]：

爱因斯坦在广义协变原理的指导下成功创立广义相对论，乃至他后来对统一场论的执着，充分体现了他对自然定律美的信心。他在创立广义相对论的论文里写道 [49]：

对于物理学之美的追求贯穿了杨振宁的研究工作 [50]，也反映在他对非阿贝尔规范理论的执着。杨振宁曾经感叹 [34]:

泡利对规范理论的态度的演变则反映了他求真的一丝不苟。在泡利去世60周年之际，我们向这位天才大师致以深深的敬意。

非阿贝尔规范理论的美使得1954年的杨振宁相信它包含一定程度的真,尽管暂时不能解决规范粒子质量问题。杨振宁和米尔斯的论文最后关于这个问题的讨论和结论“我们不能对b量子（译注：指规范粒子）的质量作出任何结论” [31]富有预见性，因为后来发现规范粒子可以通过规范对称自发破缺而获得质量（W±和Z0），也可以无质量（胶子）。将来标准模型被超越后，很可能规范理论依然重要。 

规范理论最初提出后立即被否定，后来得到重生；非阿贝尔规范理论提出后立即遭到质疑，后来在加入其他思想元素后得到复兴，成为粒子物理标准模型的构架。历史表明，美与真能否统一，由实验决定。同样，理论的进一步发展，比如弄清规范对称自发破缺的奥秘、探索规范对称的起源、搞懂为什么中微子质量不为零，等等，也需要实验的进步。 

本文在《物理文化与施郁世界线》（Physicalculture）分章转载。

制版编辑 | 皮皮鱼

更多精彩文章：

施郁：霍金为何不朽

如何成为并辞去美国科学院院士 | 费曼百年（上）

点击“阅读原文”，与知识分子一起悦读2019。