撰文 | 张天蓉
责编 | 张天祁
美丽的对称无处不在,从遍布大自然的虫草花鸟,到缥缈浩瀚的宇宙星辰,以及绚丽多彩灿烂辉煌的人类文化,处处都有对称之美。自然界和人类社会的事物,无一不体现出对称的和谐与美妙。而对称在理论物理中也扮演着非常重要的角色。我们常说到爱因斯坦的统一梦,他要统一什么呢?何谓统一?物理理论的统一其实就是找到一个符合一定规律的数学框架,把所有的东西都能框在里面。物理学家热衷于对称性,大自然和物理理论也的确符合多种对称性。因此,所谓的统一就是在理论中发掘更多的对称性。这篇文章对现代物理中与对称有关的一些概念,诸如群论、诺特定理、对称破缺、宇宙演化中的对称等作一简单介绍。
● ● ●
对称性,数学家怎么说
几何图形的对称不难理解,当人们说到“故宫是左右对称的”,“地球是球对称的”,“雪花是六角形对称的”等等时,每个人都懂得那是什么意思。
不过,数学家有他们特殊的语言来描述对称。例如,从数学的角度来看待刚才的几个例子,对称意味着几何图形在某种变换下保持不变。比如说,故宫的左右对称意味着在镜像反射变换下不变;球对称是说在三维旋转变换下的不变性;雪花六角形对称则是说将雪花的图形转动60、120、180、240、300度时图形不变。听起来十分有趣,原来对称是上帝设计世界时偷懒的花招之一:利用镜像对称,他只需要设计一半!利用六角形对称,他的雪花图案只需画出六分之一!球对称的天体就更好办了,画出了一个方向的景色,就让它们去绕着一个固定点不停地转圈!
上帝这种偷懒办法让人类欣赏和喜爱,誉之为对称之美。科学家们更是感觉深奥无比而对其探索不止。他们发明出了一套又一套的理论来描述对称。群论,便是描述对称的一种最好的数学语言。例如,简单的镜像对称用反射群描述;雪花的对称群叫做D6,是二面体群的一种;球对称的天体,则可以用3维旋转群SO3描述。
对称不一定只是表现在物体的外表几何形态上,也可以表现于某种内在的自然规律中。许多物理定律的表述都呈对称形式。最简单的例子,牛顿第三定律说:作用力等于反作用力,它们大小相等、方向相反,两者对称。电磁学中的电场和磁场,彼此关联相互作用,变化的电场产生磁场,变化的磁场产生电场,也是一种对称。
用数学语言定义对称的优越性之一在于容易推广。无论是外观几何的对称,还是内在特性的对称,都抽象成同样的数学语言来描述。例如,将对称概念用于物理研究中的情形,一般被表述为:如果某种变换能够保持系统的拉格朗日量不变,从而保持物理规律不变的话,就说系统对此变换是对称的。
物理规律应该在变换中保持不变,这应该是显而易见的。试想,如果今天的某个定律明天就不适用了,或者是万有引力定律在纽约适用,搬到上海就不对了,那还叫做自然规律吗?研究它有意义吗?当然不应该是这样的。
刚才举的例子中,今天到明天、纽约到上海,这两个概念都称之为数学变换。前者叫时间平移变换,后者叫空间平移变换。除了平移变换之外,还有许多别的种类的变换,这些变换之间有些什么样的关系呢?
物以类聚,人以群分。各种变换也可以用数学上的“群”来加以分类。所以,变换用以描述对称,群描述变换,群和对称,便如此关联起来了。
此文不深究“群” 在数学上的严格定义,只是简单地用一句话来概括:群就是一组元素的集合,在集合中每两个元素之间,定义了符合一定规则的某种乘法运算规则。这儿所说的“乘法”是广义的,并不限于通常意义上的乘法。实际上,群论中的“乘法”,只是两个群元之间的某种“操作”而已。这种“乘法” “操作”不一定可交换(或称对易),乘法可对易的“群”叫做“阿贝尔群”,不对易的“群”叫做“非阿贝尔群”。
群中的元素满足群的4个基本要求,可将它们简称为“群4点”。
1. 封闭性:两元素相乘后,结果仍然是群中的元素;
2. 结合律:(a*b)*c = a*(b*c);
3. 单位元:存在单位元(幺元),与任何元素相乘,结果不变;
4. 逆元:每个元素都存在逆元,元素与其逆元相乘,得到幺元。
欧拉最早有了群的模糊概念,但“群”这个名词以及基本设想,是法国数学家,少年天才伽罗瓦提出的。伽罗瓦生活坎坷且无端卷入一场纠纷,最后在决斗中饮弹身亡。他短短20年生命所作的最重要工作就是开创建立了“群论”这个无比重要的数学领域。
群的概念不限于“有限”,其中的“乘法”含义也很广泛,只需要满足群4点即可。
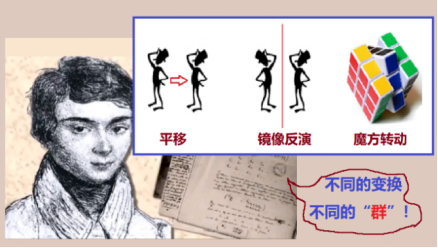
图1:各种操作都可以被定义为“群”乘法,只要符合“群4点”。
如果你还没有明白什么是“群”的话,那就再说得通俗一点:“群”就是那么一群东西,我们为它们两两之间规定一种“作用”。两两作用的结果还是属于这群东西;其中有一个特别的东西,与任何其它东西作用都不起作用;此外,每样东西都有另一个东西和它抵消;最后,如果好几个东西接连作用,只要这些东西的相互位置不变,结果与作用的顺序无关。
群的例子包括离散群、连续群、有限群、无限群、阿贝尔群、非阿贝尔群……。
空间中的旋转构成群,是物理中非常重要的一类群。物理学与各种旋转结下不解之缘,从力学中研究的刚体转动,到量子理论中的粒子自旋。地球绕太阳转,月亮绕地球转,滚珠在轴承滚道中转,电子绕原子核转,宇宙中的星云,我们居住的地球,太阳系和银河系,这些天体都处于永恒而持久的旋转运动中。每一层次的实验和理论中似乎都少不了旋转。物理中的旋转除了在真实时空中的旋转之外,还有一大部分是在假想的、抽象的空间中的旋转,比如动量空间,希尔伯特空间,自旋空间、同位旋空间等。
旋转群有离散的和连续的之分。理论物理,特别是统一理论中所感兴趣的连续旋转群有SO(3)、SO(2)、U(1)、SU(2)、SU(3)等等[1]。
可以用矩阵的语言解释上面一串旋转群的符号:每个符号括号中的数目字(3、2、1)等是表示旋转的矩阵空间的维数;大写字母O(Orthogonal)代表正交矩阵;U(Unitary)代表酉矩阵;S(Special)是特殊的意思,表示矩阵的行列式为1。
比如,举三维空间的旋转群O(3)为例。这儿3是指旋转空间的维数,O对应于保持长度和角度不变的正交变换矩阵。具体一点说,O(3)可以由一个3X3=9个实数组成的正交矩阵来表示。一般来说,正交矩阵O(3)的行列式可为1或-1。当行列式为-1时,正交矩阵表示的变换是旋转再加反演,这儿的负号便来自反演。将O(3)旋转群的行列式限制为1,指的便是特殊旋转群,记为SO(3)。所以,SO(3)表示的是3维空间中无反演的纯粹旋转。
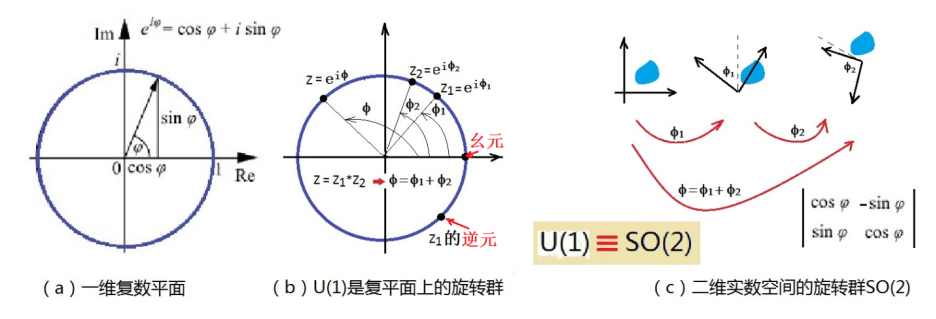 图2:U(1)群和SO(2)群
图2:U(1)群和SO(2)群
物理学中的量子理论与复数关联密切,因此量子论中将正交群的概念从实数扩展到复数,正交群O(n)便扩展成为元素为复数的酉群U(n)。行列式限制为实数1的酉群被称为特殊酉群,记为SU(n)。举例之:U(1)是1维复数空间的旋转群;SU(2)和SU(3)分别是2维和3维复数空间的特殊旋转群。
一个复数由两个实数组成,可以表示成二维实数空间中的一个点。U(1)群的元素包括模为1的所有复数,可以表示为:u= eif。尽管复数u的模为1,但幅角f还可以任意变化,所以U(1)是由复数平面上所有长度为1的矢量绕着原点转动形成的单位圆构成的。
所以, U(1) 与SO(2)同构,SU(2)和SU(3)也有相关的实数群,不过关系比较复杂。例如, SU(2)与SO(3) 两个群不是同构的,它们之间存在的是2:1的同态关系。
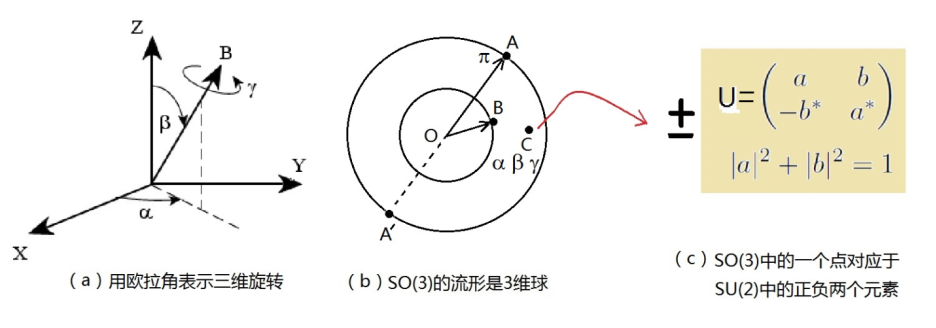 图3:SU(2) 群和SO(3)群
图3:SU(2) 群和SO(3)群
1986年,费曼在一次演讲中生动地解释与SU(2)相对应的电子自旋,他身体力行,模拟演示了一段水平放置的杯子在手臂上的旋转过程,如图4所示。费曼当时以风趣的语言及精彩的表演,赢来掌声一片。
 图4:费曼演示:在三维空间旋转360度,不能复原!
图4:费曼演示:在三维空间旋转360度,不能复原!
量子物理中,电子的自旋不是一个矢量,物理学家们以“旋量”来称呼它。当3维空间中旋转360度时,自旋群SU(2)中的元素只旋转180度,与缪比乌斯带的拓扑性质有类似之处。有趣的是,在真实世界中也存在这种现象,旋转360度不一定能恢复原来的状态!狄拉克最早设计了一个剪刀实验(图5),由费曼奇妙的旋转演示表明的,便是这种情形。杨振宁先生研究的非阿贝尔规范场,也是相关于SU(2)群的对称性。
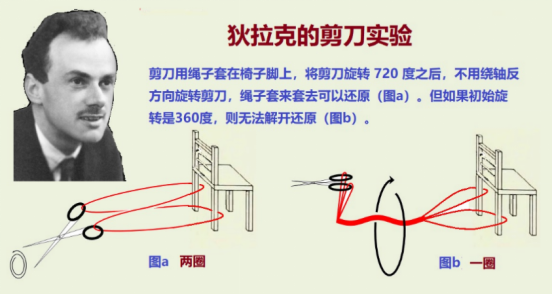
图5:狄拉克的剪刀实验
目前物理学中担任统一角色的“标准模型”,便是将所有61种基本粒子及3类相互作用,统一在规范群SU(3)×SU(2)×U(1)的框架中。由此可见对称及群论于物理学的重要意义。
女科学家揭开守恒定律奥秘
除了贡献于统一理论之外,对称在物理中有更为广泛更为深刻的内在意义。揭示这点的是一位杰出的德国女数学家:艾米·诺特。她不仅对抽象代数作出重要贡献,也为物理学家们点灯指路,她有关对称和守恒的美妙定理,揭开了大自然规律中一片神秘的面纱。
艾米·诺特(Emmy Noether ,1882-1935)有犹太血统。她数学功力深厚、科研才华洋溢,曾经受到外尔、希尔伯特、及爱因斯坦等人的高度赞扬。当年的希尔伯特为了极力推荐诺特得到大学教职,曾用犀利的语言嘲笑那些性别歧视的学究们说:“大学又不是澡堂!”
诺特对理论物理最重要的贡献是她的“诺特定理”[2]。这个定理将对称性与物理学中的守恒定律联系起来。表面上看起来,对称性描述的是大自然的数学几何结构,守恒定律说的是某种物理量的变化规律,两者似乎不是一码事。但是,这位数学才女却从中悟出了两者间深刻的内在联系。
诺特定理是理论物理的中心结果之一,它表达了每个连续可微对称性,都存在一个对应的守恒流,有着相应的守恒定律。这个定理对于所有基于作用量原理的物理定律是成立的,特别是和量子力学深刻相关,因为它仅用经典力学的原理就可以认出和海森堡测不准原理相关的物理量,如位置与动量,时间与能量。
应用诺特定理,可以帮助物理学家在一般理论中通过分析各种使得所涉及的定律的形式保持不变的变换而获得深刻的洞察力。例如:
首先,在经典理论中,物理系统对于空间平移不变的对称性,给出了动量守恒律;对于转动的不变性给出了角动量守恒律;对于时间平移的不变性给出了能量守恒定律。
在量子场论中,诺特定理被推广而成沃德-高桥恒等式,它由理论的全域或规范对称性来联系不同的关联方程,产生出更多的守恒定律,例如从电势的规范不变性得出电荷守恒。
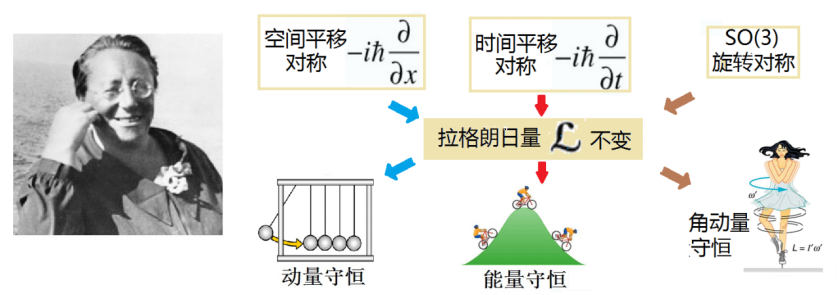
图6:艾米·诺特和诺特定理
诺特是女科学家中的佼佼者,她的父亲当年是一位颇有名气的数学教授。但尽管如此,在男性主导的学术界中,诺特的求学及科研之路一直充满了坎坷。诺特于1907年获得数学博士学位,1918年证明了“诺特定理”。即便是这个当年被多位数学大师们都认可的重要成果,也是由数学家克莱因在皇家科学院的会议上代她作的报告,因为诺特是女性,没有资格在这个会议上发言!之后,在赫尔曼·外尔等的帮助下,她1922年到哥廷根大学执教,但却再次因为是女性的缘故不能光明正大地拿薪资。1933年二战期间,由于她的犹太血统,被德国纳粹驱逐出境,流亡到了相对而言更为开放的美国,在宾夕法尼亚州的布林莫尔学院得到一个教职。
当年的诺特对美国的生活方式充满了好奇,新环境下她活力四射热情洋溢。但不幸的是,她还没来得及充分利用这优越的学术氛围做出更多成果便因病早逝了。在1935年的春假期间,诺特做了一个腹部的常规手术并患上了并发症,几天内就去世,结束了她短暂而快乐的美国之旅,终年53岁。
爱因斯坦给《纽约时报》的悼词中称赞艾米·诺特是“自女性开始接受高等教育以来,迄今为止诞生的最具创造性的数学天才。”,由爱因斯坦之言,可见“诺特定理”在理论物理界的重要性。
对称性在数学上表示某种不可分辨性,因此也意味着物理上某个力学量不因测量而改变。这样就很自然地将对称与守恒联系起来,而诺特定理,则为这种联系奠定了理论基础。
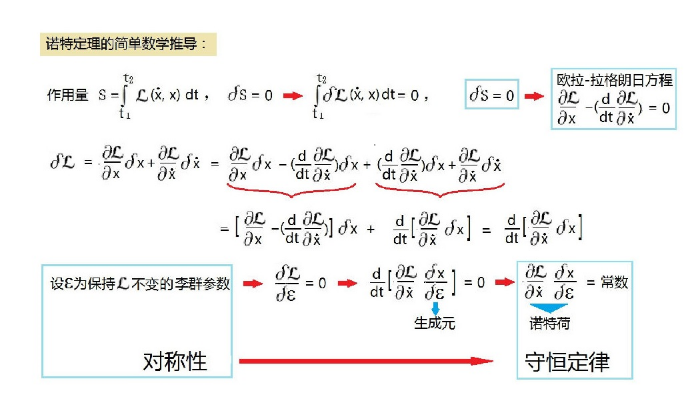
图7:诺特定理的简单推导
诺特定理的证明不易理解,图7给出一个简单推导的思路。
诺特定理在宇宙暴胀论、广义相对论和量子力学、弦理论和万有理论中都发挥了基础性数学物理学的价值,每一个物理的对称性都包含了一个守恒量,反之亦然。它构成了粒子物理中标准模型的基础,并使物理学中的守恒定律超越了经验规则,被赋予了更深层次的理论意义。
总之,现代物理学及统一场论中,对称和守恒似乎已经成为物理学家们探索自然奥秘的强大秘密武器。感谢诺特这位伟大的女性,为我们揭开了数学和物理之间这个妙不可言的神秘联系。
“非对称创造了世界”
现代物理学之奇妙之处,不仅仅体现在发现了对称,还体现在发现了“对称破缺”。
不是说对称之美吗,为何又要“破缺”呢?其实,有对称又有不对称还加破缺,方为真美大美!你想想看,如果大千世界中处处都是标准的对称:太阳和月亮像是圆规画出来的;高低不一蜿蜒连绵的群山变成了一个个等腰三角形;每个人的脸部都严格地左右对称……如此的世界不是显得太单调了毫无情趣可言吗?当然也谈不上能产生多少美感了。仔细观察我们周围实际的世界:人和动物的左脸并不完全等同于右脸;大多数人的心脏长在左边,大多数的DNA分子是右旋的;地球并不是一个完全规则的球形,等等,存在许多不对称的事实。而正是因为对称中有了这些不对称的元素,对称与不对称的和谐交汇,才创造了看起来如此美丽的世界。
本文中我们仅从物理学中的“对称破缺”这个术语,来探索一下产生不对称的深层原因。
大自然这个“上帝”是很聪明的,它在创立物理定律时比较注意不偏不倚,否则叫人类如何去认识自然规律呢?但上帝并不是将人类当成左右不分的痴呆者,自然规律要简单,世间万物却需要五彩缤纷。在创造世界万物的时候,上帝更是充分发挥他的创造力和想象力,否则,“万物之灵”的生命就不会产生了。
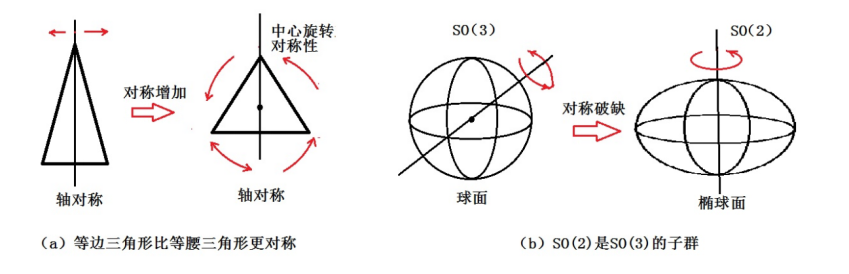
图8:对称性的不同等级
首先不妨深究一下对称的种类,各种对称有等级吗?对称确有不同的等级,例如,就几何图像而言,具有某种变换下的对称,但对另一种变换便可能不对称。即使是同一类型的对称,也有对称程度的高低之分。比如,一个正三角形,和一个等腰三角形比较,正三角形应该更为对称一些,如图8a。再举旋转群为例:一个球面是三维旋转对称的,在SO(3)群作用下不变,而椭球面只能看作是在二维旋转群SO(2)的作用下不变了。用不很严格地说法,SO(2)是SO(3)的子群,因此,球面比椭球面具有更多的对称性,见图8b。
现在我们便可以定义“对称破缺”了:如果从对称性的高低等级来定义的话,系统从对称性高的状态,演化到对称性更低的状态,便是“对称破缺”,反之则可称为“对称建立”。例如,当正三角形变形为等腰三角形,或者当球面变成椭球面,我们便说“对称破缺了”。从群的观点来看,SO(3)是3阶的,SO(2)只是1阶对称,所以,从球面到椭球面, 2个对称性被破缺了。仿照上面的例子,物理学家们便从群论的观点来研究对称破缺。
例如,物质的相变也是一种对称破缺(或提升)。物质三态中,液态比晶体固态具有更高的对称性。液态分子处于完全无序的状态,处处均匀,各向同性,凝固成固态后,分子有次序地排列起来,形成整齐漂亮的晶格结构。因此,从液态到固态,有序程度增加了,而对称性却降低了,破缺了。
“对称性的破缺”可以分为两大类:明显对称破缺和自发对称破缺。
明显的对称破缺:系统的拉格朗日量明显违反某种对称性,因而造成物理定律不具备这种对称性。弱相互作用的宇称不守恒,便是属于这一类。
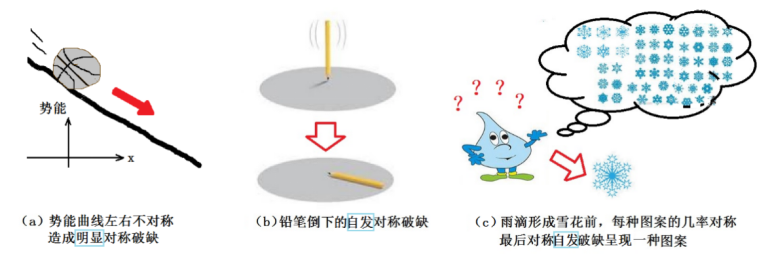 图9:自然界的明显对称破缺和自发对称破缺
图9:自然界的明显对称破缺和自发对称破缺
自发对称破缺又是什么意思呢?它指的是物理系统的拉格朗日量具有某种对称性,但物理系统本身却并不表现出这种对称性。换言之,物理定律仍然是对称的,但物理系统实际上所处的某个状态并不对称。图9中举了几个日常生活中的例子来说明对称性的“破缺”。
图9a中所示是一个在山坡上的石头,山坡造成重力势能的不对称性,使得石头往右边滚动,这是一种明显对称性破缺。在图9b的情况,一支铅笔竖立在桌子上,它所受的力是四面八方都对称的,它往任何一个方向倒下的几率都相等。但是,铅笔最终只会倒向一个方向,这就破坏了它原有的旋转对称性。这种破坏不是由于物理规律或周围环境的不对称造成的,而是铅笔自身不稳定因素诱发的,所以叫自发对称破缺。图9c的水滴结晶成某个雪花图案的过程也属于自发对称性破缺。
最早从物理学的角度来探索非对称性和对称破缺的,是法国物理学家皮埃尔·居里(Curie,著名居里夫人的丈夫)。皮埃尔说:"非对称创造了世界” 。后来,皮埃尔发现了物质的居里点,当温度降低到居里点以下,物质表现出自发对称破缺。例如,顺磁体到铁磁体的转变属于这种对称破缺。在居里温度以上,磁体的磁性随着磁场的有无而有无,即表现为顺磁性。外磁场消失后,顺磁体恢复到各向同性,是没有磁性的,因而具有旋转对称性。当温度从居里点降低,磁体成为铁磁体而有可能恢复磁性。如果这时仍然没有外界磁场,铁磁体会随机地选择某一个特定的方向为最后磁化的方向。因此,物体在该方向表现出磁性,使得旋转对称性不再保持。换言之,顺磁体转变为铁磁体的相变,表现为旋转对称性的自发破缺。
如今看起来,自发对称破缺的道理不难理解,但当初却曾经困惑物理学家多年。自发对称破缺就是说,自然规律具有某种对称性,但服从这个规律的现实情形却不具有这种对称性,因而在实验中没有观察到这种对称性,理论似乎与实验不符合。如用数学语言描述,就是系统的方程具有某种对称性,但方程的某一个解不一定要具有这种对称性。一切现实情况下的实验结果,是系统“自发对称破缺”后的某种特别情形。它们只能表现方程的某一个解,反映的只是物理规律的一小部分侧面。
继皮埃尔·居里之后,前苏联物理学家朗道和金斯堡用对称自发破缺来解释超导。美国物理学家安德森扩展了他们的工作。后来,日裔美国物理学家南部阳一郎(1921年 -)首先将“对称破缺”这一概念从凝聚态物理引进到粒子物理学中[3]。南部为此和另外两位日本物理学家,分享了2008年的诺贝尔物理奖。
凝聚态物理和粒子物理,初看似乎是两个风马牛不相干的两个领域,在研究时所涉及的能量级别上也相差几百亿倍,但它们在本质上却有一个共同之处:研究的都是维数巨大的系统,这是自发对称破缺发生的必要条件。
自发对称破缺的原因,是因为量子态的简并。我们也可以从上面所说的经典例子来理解这点。比如说图9b所示的铅笔,上图中的铅笔的平衡位置,是一个能量较高的不稳定状态,倒下去之后躺在桌子上的状态能量最低,可以看作是某种稳定的“基态”。因为铅笔可以向任何一个方向倒下,因而基态不止一个,而是有无穷多个。也就是说,铅笔的“基态”是“简并”的,无限多的。就“基态”的整体而言,是和物理规律一样具有旋转对称性,但是铅笔往一边倒下后,便只能处于一个具体的“基态”,那时旋转对称性就破缺了。
对称破缺,解释宇宙起源的秘密
世界为什么是现在这个样子,而不是别的状态?从物理学的角度思考这个问题,带给我们很多疑问,但如上所述的对称理论可以给我们部分解释。
比如说,宇宙的早期,没有星球,没有原子、分子、电子,整个世界是混沌的一团,现有的四种相互作用力也表现为一种统一的形式。也就是说,在大爆炸后的极早期,宇宙是完全对称的,作用力是统一的,之后为什么会分裂成4种不同的相互作用呢?
这是因为自发对称破缺在宇宙演化中扮演了一个重要的角色。
对称破缺是我们现在的宇宙起源和存在的原因。时间和空间、天体、物质、生命、大自然,世界上的一切,都是对称破缺的产物。

图10:大爆炸后,由于不断的自发对称破缺而形成现在的宇宙
如图10所示,大爆炸发生之后,随着温度下降,对称破缺,引力作用首先分离出来,然后是强作用力的分化,剩下了弱电统一,当宇宙继续变冷,弱电统一也开始破缺,形成现在我们熟知的四种力。再后来,宇宙开始了大范围的变化,由于对称性自发破缺形成了各种基本粒子,基本粒子又由于各种力的相互作用而结合成更为复杂的原子、分子、星球、星系等,直到产生生命,最终完成了现在所观察到的宇宙图景。
可以举希格斯机制赋予粒子质量为例。场的真空态是能量最低的状态。但是一般来说,能量最低的状态对应于场强为0。如果场的势能曲线比较特别,比如通常经常使用的所谓“墨西哥帽子”的形状(图11c)。这时,能量最低的状态是无限简并的,即墨西哥帽向下凹的一圈。这一圈的能量最低,但场强却不为0。希格斯场的真空态,便可以由这种势能曲线描述的系统,产生“自发对称破缺”而得到。因此,真空中存在着场强非零的、稳定的希格斯场。这种场无处不在,无孔不入,质量为零的各种基本粒子身陷其中,与希格斯场相互作用,并且获得它应该具有的质量。
从现代场论的观点,场的激发态便表现为粒子。希格斯场的真空态有4种激发模式(图11c的左上图),其中沿着势能曲线对称轴绕圈的相位变化模式有3种,对应于3种质量为0的Goldstone粒子,这些粒子在与其它粒子反应时消失不见,叫做被“吃”掉了,只有一种沿着势能曲线“径向”振动的激发模式对应于有质量的场粒子,也就是被大家称之为“上帝粒子”的希格斯粒子。
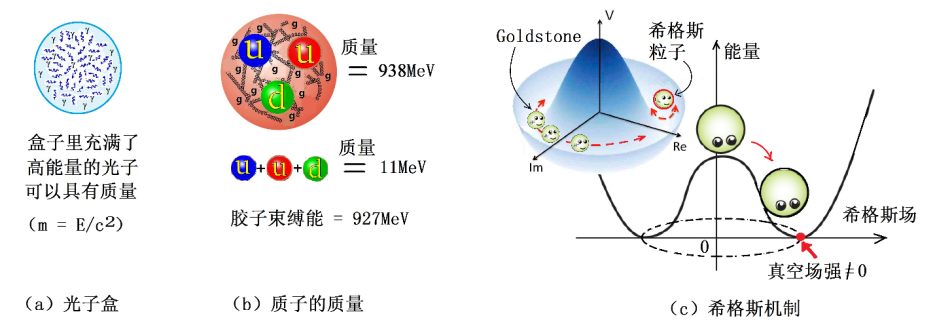
图11:质量来源于真空自发对称破缺
综上所述,希格斯粒子解决了质量的问题,物理学家们得以在杨-米尔斯规范场的基础上建立理论,将除了引力之外的其它三种力,统一在同一个标准模型中。标准模型包括了61种基本粒子,而希格斯粒子是这些粒子中,最后一个被“发现”的。这是验证标准模型的一个重要里程碑。
宇宙中正物质和反物质的数量比例是另一个使物理学家们困惑的问题。
狄拉克将正电子的假设带进了物理学,安德森1932年证实了正电子的存在,1955 年,赛格雷和张伯伦发现了反质子;第二年, 美国物理学家考克发现了反中子。反粒子的发现使人们对物质世界的思考多了一个方向:反世界。狄拉克曾经猜测,宇宙中完全有可能存在由反物质组成的星球。但是人们从来没有在实验室及天文观测中发现反世界的迹象。
如果说创世之初,当宇宙开始的时刻,一切都是对称的、中性的话,后来也应该产生等量的物质和反物质。但是,我们放眼望去,一直望到我们能够看到的整个宇宙,也只是看见与我们的世界相类似的“正物质”组成的天体。为什么大爆炸后形成的世界中只有这些正物质而没有反物质呢?成对产生的另一种反粒子到哪儿去了?我们当然并不欢迎它们回来,因为那样会与我们的世界“湮灭”而毁灭一切。但是,好奇心使科学家们一直思考这个问题。物理学家认为这也是由自发对称破缺造成的,最后,2008年诺贝尔物理奖得主中的两位日本物理学家小林诚和益川敏英在这个方向上迈出了第一步。
1973年,29岁的小林诚和33岁的益川敏英提出了“小林-益川理论”,解释宇宙演化过程中粒子多于反粒子的原因[4]。他们研究了弱相互作用中CP对称性的破坏,认为粒子和反粒子之间除了电荷符号不同之外,还有一些微小的差异,这个微小差异引起CP自发对称破缺,从而使得正粒子和反粒子衰变反应的速率不同,之后造成正粒子数目大大多于反粒子。根据他们的理论,应该存在6种夸克,这种对称破缺机制才能起作用,而当时只发现了3种夸克,被预言的另外3种夸克分别在1974、1977、1995年被发现。
 图11:2008年诺贝尔物理奖得主
图11:2008年诺贝尔物理奖得主
此外,在2001年和2004年,美国斯坦福实验室和日本高能加速器分别独立地实现了小林-益川理论所描述的自发对称破缺机制,这些极为引人注目的实验证据让他们和南部阳一郎一起,获得了2008年的诺贝尔物理奖。
对称和对称破缺的概念,像一剂又一剂的灵丹妙药,物理研究中的很多疑问都可用它们来解释。欲了解更多物理中的统一理论与对称的关系,请参考其它参考文献[5,6]。
作者张天蓉,系理论物理学博士,职业科普作家。
参考文献:
【1】B. G. Wybourn , “Classical Groups for Physicists”, Wiley ,NewYork, (1974)
【2】Kosmann-Schwarzbach, Yvette (2010). The Noether theorems:Invariance and conservation laws in the twentieth century. Sources and Studiesin the History of Mathematics and Physical Sciences. Springer-Verlag.
【3】Nambu Y, Jona-Lasinio G. Dynamical Model of Elementary Particles Based on an Analogy with Superconductivity. I [J]. Physical Review, 1961, 122: 345–358.
【4】Kobayashi M, Maskawa T. CP-Violation in the Renormalizable Theory of Weak Interaction[J]. Progress of Theoretical Physics,1973, 49 (2): 652–657.
【5】文小刚,我们生活在一碗汤面里吗?——光和电子的统一与起源.[J/OL]. Physics, 41(06): 359-366. , 2012.
【6】张天蓉,走向统一:粒子物理之路[M].北京:清华大学出版社,2022.,
0
推荐




 京公网安备 11010502034662号
京公网安备 11010502034662号 