撰文 | 张天蓉 （美国德州大学奥斯汀分校理论物理博士）

责编 | 吕浩然

 

●　●　●

 

上一篇中，通过赌徒谬误介绍了概率论中的大数定律。大数定律说的是当随机事件重复多次时频率的稳定性，随着试验次数的增加，事件发生的频率趋近于预期的“概率”。但大数定律并未涉及概率分布问题，所以本文就来说说概率分布。首先，用如下例子来说明“概率分布”是什么意思。 

 

高尔顿钉板试验

 

弗朗西斯·高尔顿（Sir Francis Galton，1822-1911）是英国著名的统计学家、心理学家和遗传学家。他是达尔文的表弟，虽然不像达尔文那样声名显赫，但也并非无名之辈。不仅如此，高尔顿幼年是神童，长大是才子，九十年的人生可谓丰富多彩，是个名副其实的博学家。其涉猎范围广泛，研究水平颇深，纵观科学史，在其同时代科学家中，能望其项背之人寥寥可数【1】。

 

在达尔文发表了《物种起源》之后，高尔顿也将研究方向转向生物及遗传学，他第一个对同卵双胞胎进行研究，论证了指纹的永久性和独特性；他从遗传的角度研究人类智力并提出“优生学”，也是第一个强调把统计学方法应用到生物学中去的人；他还设计了一个钉板实验，希望从统计的观点来解释遗传现象。

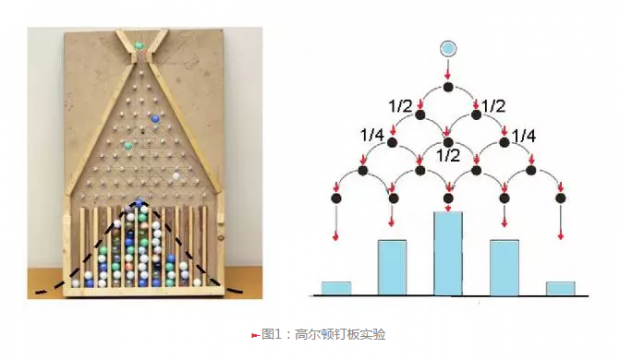
如图1中所示，木板上订了数排（n排）等距排列的钉子，下一排的每个钉子恰好在上一排两个相邻钉子中间，从入口中处放入若干直径略小于钉子间距的小球，小球在下落的过程中碰到任何钉子后，都将以1/2的概率滚向左边，也以 1/2的概率滚向右边。如此反复地继续下去，直到小球下落到底板的格子里为止。试验表明，只要小球足够多，它们在底板堆成的形状将近似于一个钟形的高斯曲线（图1左下黑色曲线）。

 

为什么这儿出现了一个钟形曲线呢？这与古典概率论中最重要的“中心极限定理”有关。

 

中心极限定理

 

事实上，中心极限定理不是一个定理，而是一组定理，分别适用于不同的条件。但基本可以用一句话来概括它们：大量相互独立的随机变量，其求和后的平均值以正态分布（即钟形曲线）为极限。

 

以上所述的高尔顿钉板实验显示的“钟形曲线”便可以用中心极限定理来解释。

 

考虑钉板中的某一个小球下落的过程：小球在下落过程中碰到n个钉子上，每次都等效于一次“抛硬币”类型的随机变量。也就是说，一个小球从顶部到底部的过程，等效于n次抛硬币之和。n个钉子中的每一个钉子，将小球以同等的概率弹向左边或右边，小球最后到达的位置，是这n个“左/右”随机变量相加后的平均位置。不难看出，这个平均值落在中心处的概率最大（即小球聚集最多），但也可能向左或向右偏离1格、2格……偏离越大，小球的数目越少，不同位置的小球数便形成了一个“分布”，中心极限定理则是从数学上证明了，这个分布的极限是正态分布。

 

中心极限定理最早由法国数学家棣莫弗（de Moivre， 1667-1754）在1718年左右发现。他为解决朋友提出的一个赌博问题而去认真研究二项分布（每次试验只有“是/非”两种可能的结果，且两种结果发生与否互相对立）。他发现：当实验次数增大时，二项分布（成功概率p=0.5）趋近于一个看起来呈钟形的曲线。后来，著名法国数学家拉普拉斯对此作了更详细的研究，并证明了p不等于0.5时二项分布的极限也是高斯分布。之后，人们将此称为棣莫弗-拉普拉斯中心极限定理【2】。

 

再后来，中心极限定理的条件逐渐从二项分布推广到独立同分布随机序列（指随机过程中，任何时刻的取值都为随机变量，如果这些随机变量服从同一分布，且互相独立，那么这些随机变量就是独立同分布），以及不同分布的随机序列。因此，中心极限定理不是只有一个定理，而是成为研究某种条件下独立随机变量之和的极限分布为正态分布的一系列命题的统称。 

 

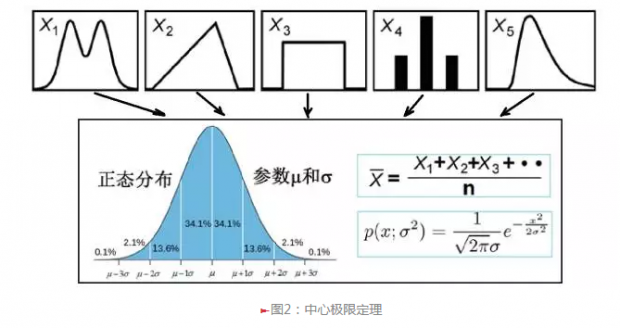
不得不承认中心极限定理的奇妙。在一定条件下，各种随意形状概率分布生成的随机变量，它们加在一起的总效应，是符合正态分布的。这点在统计学实验中特别有用，因为实际上的随机生物过程或物理过程，都不是只由一个单独的原因产生的，它们受到各种各样随机因素的影响。然而，中心极限定理告诉我们：无论引起过程的各种效应的基本分布是什么样的，当实验次数 n 充分大时，所有这些随机分量之和近似是一个正态分布的随机变量（图2）。

 

在实际问题中，常常需要考虑许多随机因素所产生的总影响。例如，许多因素决定了人的身高：营养、遗传、环境、族裔、性别等等，这些因素的综合效果，使得人的身高基本满足正态分布。另外，在物理实验中，免不了有误差，而误差形成的原因五花八门，各种各样。如果能够分别弄清楚产生误差的每种单一原因，误差的分布曲线可能不是高斯的。但是，当所有的误差加在一起时，实验者通常得到一个正态分布。

 

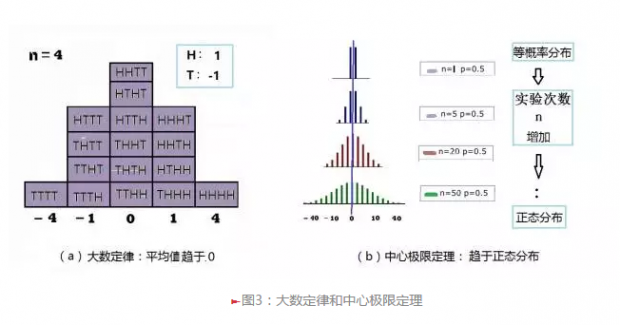
为了更为直观地理解大数定律和中心极限定理，在图3中，将抛硬币所得的结果用数值表示（正面=1，反面=-1）。如此赋值以后，大数定律指的是：抛丢硬币多次（n趋近无限大）后，结果的平均值将趋近于0，即正反面出现次数相等，其数值相加而互相抵消了；中心极限定理则除了考虑平均值（等于零）之外，还考虑结果的分布情形：如图3b所示，如果只抛1次，出现正面（1）和反面（-1）的概率相等，对应于公平硬币的等概率分布，平均值为0。当投掷次数n增加，平均值的极限值仍然保持为0，但点数和之分布情形变化了，n趋近无限时，分布趋于正态分布，这是中心极限定理的内容。

 

大量的统计实验结果告诉我们：钟形曲线随处可见。我们的世界似乎被代表正态分布的“钟形”包围着，很多事物都是服从正态分布：人的高度、雪花的尺寸、测量误差、灯泡的寿命、IQ分数、面包的重量、学生的考试分数等等。十九世纪的著名数学家庞加莱（Jules Henri Poincaré，1854-1912）曾经说过【3】：“每个人都相信正态法则，实验家认为这是一个数学定理，数学家认为这是一个实验事实。”大自然造物的美妙深奥，鬼斧神工，往往使人难以理解。钟形分布曲线无处不在，其奥秘便是来自于中心极限定理。

 

中心极限定理从理论上证明了，对于大量独立随机变量来说，不论其中各个随机变量的分布函数是什么形状，也不论它们是已知还是未知，当独立随机变量的个数充分大时，它们的和的分布函数都可以用正态分布来近似。这使得正态分布既成为统计理论的重要基础，又是实际应用的强大工具。

 

就理论而言，正态分布有不少优越性：1. 两个正态分布的乘积仍然是正态分布；2. 两个正态分布的和是正态分布；3. 正态分布的傅立叶变换仍然是正态分布。正态分布只需要两个参数μ和σ就完全决定了分布的性质（见图2）。这点给实际计算带来许多方便之处，再一次体现了中心极限定理的威力。

 

中心极限定理的应用

 

正态分布在应用上非常有效，下面便举两个简单例子予以说明。

 

例1：小王到某保险公司应聘，经理给他出了一道考题：如果让你设计一项人寿保险，假设客户的数目有1万左右，被保险人每年交200元保费，保险的赔偿金额为5万元，估计当地一年的死亡率（自然+意外）为0.25%左右，那么，你会如何计算公司的获利情况？

 

小王在经理面前紧张地估算了一下：从1万个客户得到的保费是200万，然后1万人乘以死亡率，可能有25人死亡，赔偿金额为25×5万，等于125万。所以，公司可能的收益应该是200万减去125万，等于75万左右。这是小王的答案。

 

经理面露满意的笑容，但又继续问：75万只是一个大概可能的数目，如果要你大略地估计一下，公司一年内从这个项目得到的总收益为50-100万元的概率是多少，或者需要估计公司亏本的概率，你怎么算呢？

 

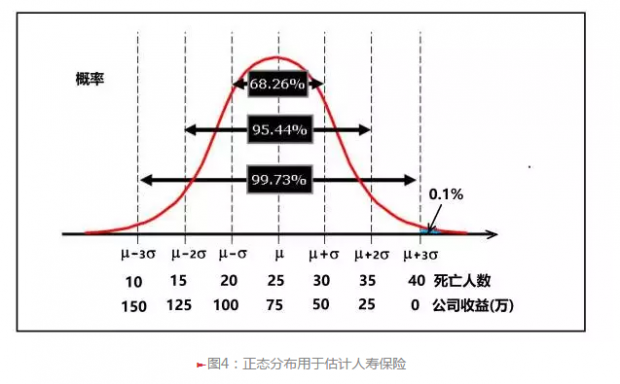
这下难倒了小王：要真正计算概率需要用到分布，这是什么分布啊？小王脑袋里突然冒出了“中心极限定理”，1万个客户的数目足够大了，可以用正态分布：首先需要计算平均值μ和方差σ。人寿保险近似于一个像抛硬币的“二项分布”问题：受保人死亡，保险公司赔偿，反之则不赔偿。只不过，这儿死亡的概率比较小，p=0.25%。用正态分布来近似的话，只要知道了期望和方差，概率便不难计算。小王回想起正态分布的简单图像以及几个关键数值（见图4），算出均值μ=E(X)=np=10000*0.25%=25，方差σ2=Var(X)=np(1-p)=25 ，由此得到σ=5。

 

然后，要计算公司赚50-100万元的概率，从图4可知，也就是死亡人数在20到30之间的概率，刚好就是从（μ-σ ）到（μ+σ ）之间的面积，大约68.2%左右。至于公司何种情况下会亏本呢？直观而言，如果死亡的人数多于40，公司便亏本了，概率到底是多少呢？同样可用图4进行估计，40和25之间相差15，等于3σ，因而得到概率大约等于0.1%，所以，保险公司亏本的概率几乎为零。

 

例2：图5a是美国2010年1,547,990个SAT考试成绩的原始数据，其中有1,313,812个分数在1850之下，有74,165个成绩是在2050以上。由此我们从原始数据可以算出：分数在1850之下的百分比是0.849，分数在2050之上的百分比是0.0479。

 

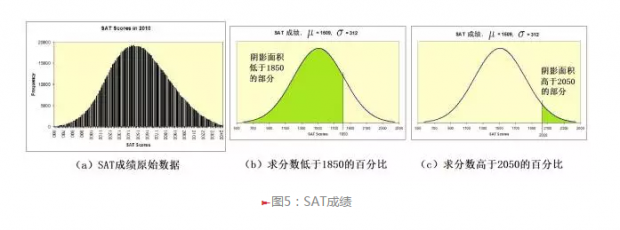
另一方面，原始的结果可以用一个平均分数μ=1509，标准方差的平方根σ=312的正态曲线来近似。因此，我们也可以从正态分布曲线来计算分数低于1850及高于2050的百分比，它们分别对应于图5b和图5c中阴影部分的面积。根据高斯积分求出两个图中的面积分别为0.8621和0.0418。对照从原始数据的计算结果0.849和0.0479，相差非常小。

 

由此可以看出，中心极限定理在现实生活中的应用非常广泛。大数定律和中心极限定理，都是基于多次实验结果的古典概率观点，属于频率学派。下一篇中将介绍概率论中极端的两大派别：频率学派和贝叶斯学派。

 

参考文献：

【1】"Sir Francis Galton F.R.S: 1822-1911". galton.org. Retrieved 9 January 2017.

【2】维基百科：中心极限定理

https://zh.wikipedia.org/wiki/%E4%B8%AD%E5%BF%83%E6%9E%81%E9%99%90%E5%AE%9A%E7%90%86

【3】Gabriel Lippmann (French physicist ,16 Aug 1845 - 13 Jul 1921), Conversation with Henri Poincaré. In Henri Poincaré, Calcul ds Probabilités (1896), 171